LeetCode.887.Super Egg Drop 鸡蛋掉落

题目描述

887 Super Egg Drop
https://leetcode-cn.com/problems/super-egg-drop/

You are given K eggs, and you have access to a building with N floors from 1 to N.

Each egg is identical in function, and if an egg breaks, you cannot drop it again.

You know that there exists a floor F with 0 <= F <= N such that any egg dropped at a floor higher than F will break, and any egg dropped at or below floor F will not break.

Each move, you may take an egg (if you have an unbroken one) and drop it from any floor X (with 1 <= X <= N).

Your goal is to know with certainty what the value of F is.

What is the minimum number of moves that you need to know with certainty what F is, regardless of the initial value of F?

Example 1:

Input: K = 1, N = 2
Output: 2
Explanation:
Drop the egg from floor 1.  If it breaks, we know with certainty that F = 0.
Otherwise, drop the egg from floor 2.  If it breaks, we know with certainty that F = 1.
If it didn't break, then we know with certainty F = 2.
Hence, we needed 2 moves in the worst case to know what F is with certainty.

Example 2:

Input: K = 2, N = 6
Output: 3

Example 3:

Input: K = 3, N = 14
Output: 4

Note:
1 <= K <= 100
1 <= N <= 10000

解题过程

谷歌的一道经典面试题，非常难，自己做出来完全不可能。第一次看题解都理解不了，第二遍看了题解后才能自己写出来。

dp[i][j] 表示有 i 个鸡蛋 j 层楼时最坏情况下的最小尝试次数
则
1、楼层数为 1 时，无论有多少个鸡蛋最小尝试次数肯定是 1
2、鸡蛋数是 1 时，有多少层楼最小尝试次数就是多少
3、对于 i>1 且 j>1 时，假如我们从第 x 楼扔鸡蛋：

如果鸡蛋不碎，那么状态变成 dp[i][j-x]，即我们鸡蛋的数目不变，但排除了 x 楼及以下的楼层，答案只可能在上方的 j-x 层楼了。
如果鸡蛋碎了，那么状态变成 dp[i-1][x-1]，即我们少了一个鸡蛋，但我们知道答案只可能在第 x 楼下方的 x-1 层楼中了

我们并不知道这个 x 是哪个楼层，所以 x 要遍历 1 到 j 层楼。
且必须保证 鸡蛋碎了之后接下来需要的步数 和 鸡蛋没碎之后接下来需要的步数 二者的最大值最小，再加上扔 x 的 1 次，就是 dp[i][j] 的值。

所以有递推公式
$$
dp[i][j] =
\begin{cases}
1, & \text{j=1} \\
j, & \text{i=1} \\
\min \limits_{1 \leq x \leq j} \big( \max ( dp[i-1][x-1], dp[i][j-x] ) \big) + 1, & \text{i>1 and j>1} \\
\end{cases}
$$

直接遍历填表的话，时间复杂度 O(kn^2) ，因为一共有 kn 个状态，且计算每个状态时 x 需要 O(n) 遍历楼层数。
会超时，只能通过 84 / 121 个测试用例。

优化
观察到 dp[i-1][x-1] 是 x 的单调递增函数， dp[i][j-x] 是 x 的单调递减函数，所以一定是在交点处 max{dp[i-1][x-1], dp[i][j-x], x = 1,...,j 最小，原因如下图：

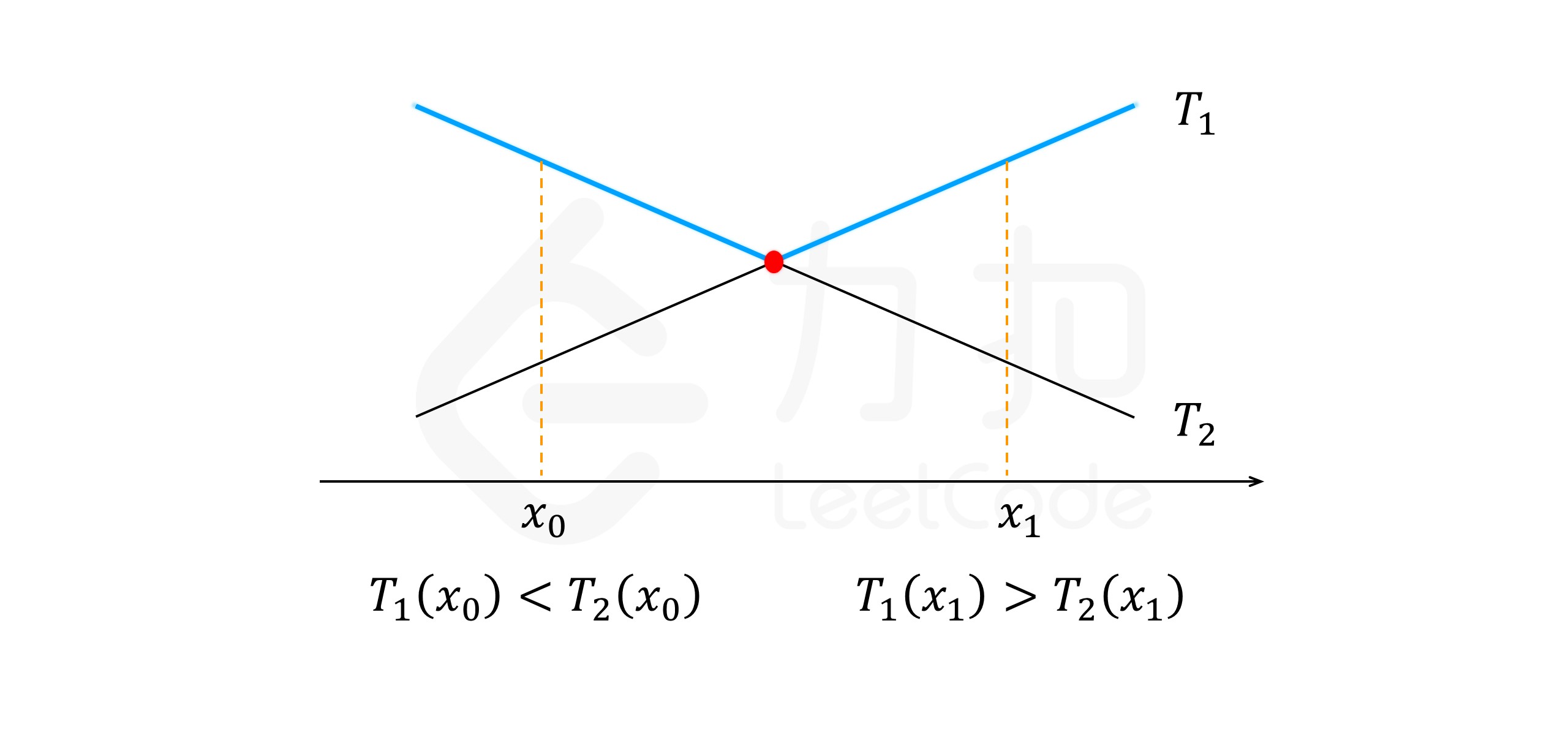
有两个单调函数， $T_1$ 单调递增， $T_2$ 单调递减，我们要求的是 $T_1$ 和 $T_2$ 的最大值中的最小值，那肯定是在交点处两个的最大值最小。由于 x 是散列的整数，所以只需要找到离交点最近的两个 x 值中的最小值，一定就是 x=1,…,j 中的最小值，且这两个 x 值肯定间隔为1，我们假设这两个 x 值分别为 $x_0$ 和 $x_1$，则 $x_1 = x_0 + 1$。
可以使用二分搜索法来确定 $x_0$ 和 $x_1$
当 dp[i-1][mid-1] > dp[i][j-mid] 时，也就是 mid 使递增函数大于递减函数，则要求的 $x_0$ 值一定在 mid 左侧，否则在 mid 右侧。

动态规划-二分搜索优化

时间复杂度 O(knlogn) ，空间复杂度 O(kn)

// 超时方法改进，二分搜索
private static class SolutionV2020BinarySearch {
    public int superEggDrop(int k, int n) {
        if (k == 1) {
            return n;
        }
        if (n == 1) {
            return 1;
        }
        // dp[i][j] 表示有 i 个鸡蛋 j 层楼时最坏情况下的最小尝试次数
        // 则有 dp[i][j] = min{max{dp[i-1][x-1], dp[i][j-x]}, x = 1,...,j} + 1
        int[][] dp = new int[k + 1][n + 1]; // 默认全为0

        // 楼层数为1时，无论有多少个鸡蛋最小尝试次数肯定是1
        for (int i = 1; i <= k; i++) {
            dp[i][1] = 1;
        }

        // 鸡蛋数是1时，有多少层楼最小尝试次数就是多少
        for (int j = 1; j <= n; j++) {
            dp[1][j] = j;
        }

        // 遍历填表
        for (int i = 2; i <= k; i++) {
            for (int j = 2; j <= n; j++) {
                // dp[i-1][x-1] 是 x 的单调递增函数， dp[i][j-x] 是 x 的单调递减函数，所以一定是在交点处 max{dp[i-1][x-1], dp[i][j-x]} 最小
                // 使用二分搜索优化 x=1,...j 的遍历
                int low = 1, high = j;
                while (low < high) {
                    if (low + 1 == high) {
                        break;
                    }
                    int mid = (low + high) / 2;
                    if (dp[i-1][mid-1] > dp[i][j-mid]) {
                        high = mid - 1;
                    } else {
                        low = mid;
                    }
                }
                int maxX = Math.max(dp[i-1][low-1], dp[i][j-low]);
                int maxX1 = Math.max(dp[i-1][low], dp[i][j-low-1]);
                int min = Math.min(maxX, maxX1);
                dp[i][j] = min + 1;
            }
        }
        return dp[k][n];
    }
}

动态规划-穷举遍历

时间复杂度 O(kn^2) ，空间复杂度 O(kn)
超时， 84 / 121 个通过测试用例

// 超时， 84 / 121 个通过测试用例
private static class SolutionV2020TimeExceed {
    public int superEggDrop(int k, int n) {
        if (k == 1) {
            return n;
        }
        if (n == 1) {
            return 1;
        }
        // dp[i][j] 表示有 i 个鸡蛋 j 层楼时最坏情况下的最小尝试次数
        // 则有 dp[i][j] = min{max{dp[i-1][x-1], dp[i][j-x]}, x = 1,...,j} + 1
        int[][] dp = new int[k + 1][n + 1]; // 默认全为0

        // 楼层数为1时，无论有多少个鸡蛋最小尝试次数肯定是1
        for (int i = 1; i <= k; i++) {
            dp[i][1] = 1;
        }

        // 鸡蛋数是1时，有多少层楼最小尝试次数就是多少
        for (int j = 1; j <= n; j++) {
            dp[1][j] = j;
        }

        // 遍历填表
        for (int i = 2; i <= k; i++) {
            for (int j = 2; j <= n; j++) {
                int min = Integer.MAX_VALUE;
                for (int x = 1; x <= j; x++) {
                    min = Math.min(min, Math.max(dp[i-1][x-1], dp[i][j-x]));
                }
                dp[i][j] = min + 1;
            }
        }
        return dp[k][n];
    }
}

GitHub代码

algorithms/leetcode/leetcode/_887_SuperEggDrop.java
https://github.com/masikkk/algorithms/blob/master/leetcode/leetcode/_887_SuperEggDrop.java

当前位置 : 首页 » 文章分类 : 算法 » LeetCode.887.Super Egg Drop 鸡蛋掉落