LeetCode.994.Rotting Oranges 腐烂的橘子

题目描述

994 Rotting Oranges
https://leetcode-cn.com/problems/rotting-oranges/

In a given grid, each cell can have one of three values:

• the value 0 representing an empty cell;
• the value 1 representing a fresh orange;
• the value 2 representing a rotten orange.

Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange.  If this is impossible, return -1 instead.

Example 1:

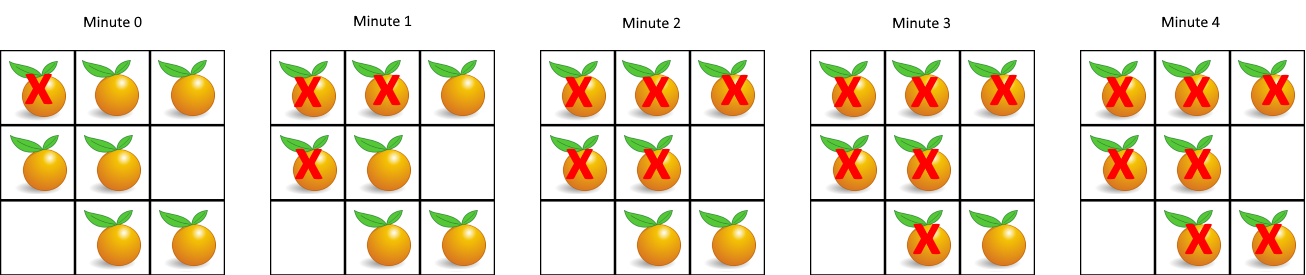
Input: [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation:  The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: [[0,2]]
Output: 0
Explanation:  Since there are already no fresh oranges at minute 0, the answer is just 0.

Note:
1 <= grid.length <= 10
1 <= grid[0].length <= 10
grid[i][j] is only 0, 1, or 2.

---

相似题目

LeetCode.994.Rotting Oranges 腐烂的橘子
LeetCode.1162.As Far from Land as Possible 离所有陆地最远的海洋/地图分析
LeetCode.542.01 Matrix 01矩阵

---

解题过程

典型的广度优先搜索。

这个题要注意，最初腐烂的橘子不只有一个。
比如测试用例 [2, 1, 1, 1, 2, 1, 1] ，从两个 2 同时开始想四周腐烂，最短仅需2步即可。

我的解法是：
从每个值为2的腐烂结点开始，一步一步的向外扩散，每次扩散时把新腐蚀的结点标为一个递增的值 2，3，4，5，每个循环都从上一次刚刚腐蚀的结点开始扩散，知道一次循环中没有新节点被腐蚀，停止循环。
则此时走过的步数就是把所有能腐蚀的全部腐蚀完需要的最小步数，如果还有结点没被腐蚀，说明无法完全腐蚀。

这个思路中的“每个循环都从上一次刚刚腐蚀的结点开始扩散”就是深度优先遍历BFS的思想。

也可以用队列实现：
起始把所有值为2的腐烂结点入队列，每次把一层结点出队，将周围的新腐烂结点入队，直到没有新腐烂的结点为止，经过的层数就是最小步数。最后还有结点没被腐蚀，说明无法完全腐蚀。

时间复杂度 O(mn)，注意方法 rot1Step() 只是向四边做一次考察，可以看做O(1)的复杂度
空间复杂度 O(1)

private static class SolutionV2020 {
    public int orangesRotting(int[][] grid) {
        int nr = grid.length, nc = grid[0].length;

        // 腐烂的步数
        int step = 0;
        // 上一步（上一分钟）是否有新腐蚀的结点，没有新腐蚀的结点则结束
        boolean newRot = true;
        while (newRot) {
            newRot = false;
            int lastRotValue = 2 + step;
            for (int i = 0; i < nr; i++) {
                for (int j = 0; j < nc; j++) {
                    // 从上次腐烂结点（值为lastRotValue）开始向周围腐烂1步，标为 lastRotValue + 1
                    if (grid[i][j] == lastRotValue) {
                        newRot = rot1Step(grid, i, j, lastRotValue + 1) || newRot;
                    }
                }
            }
            step ++;
        }

        // 若还有未腐烂的结点，返回-1
        for (int i = 0; i < nr; i++) {
            for (int j = 0; j < nc; j++) {
                if (grid[i][j] == 1) {
                    return -1;
                }
            }
        }
        return step - 1;
    }

    // 从 row,column 开始向上下左右腐烂1步，标为 newValue, 如果有新腐烂的结点返回true
    private boolean rot1Step(int[][] grid, int row, int column, int newValue) {
        int nr = grid.length, nc = grid[0].length;
        boolean ret = false;
        // 结点上下左右的新鲜结点入队
        if (row - 1 >= 0 && grid[row - 1][column] == 1) { // 上
            grid[row - 1][column] = newValue;
            ret = true;
        }
        if (column + 1 < nc && grid[row][column + 1] == 1) { // 右
            grid[row][column + 1] = newValue;
            ret = true;
        }
        if (row + 1 < nr && grid[row + 1][column] == 1) { // 下
            grid[row + 1][column] = newValue;
            ret = true;
        }
        if (column - 1 >= 0 && grid[row][column - 1] == 1) { // 左
            grid[row][column - 1] = newValue;
            ret = true;
        }
        return ret;
    }
}

---

GitHub代码

algorithms/leetcode/leetcode/_994_RottingOranges.java
https://github.com/masikkk/algorithms/blob/master/leetcode/leetcode/_994_RottingOranges.java

---