有关可变形部件模型(Deformable Part Model)的一些说明

（1）可变形部件模型

可变形部件模型(DeformablePart Model)由三部分组成：

(1) 一个较为粗糙的，覆盖整个目标的全局根模版(或叫做根滤波器)。
(2) 几个高分辨率的部件模版(或叫做部件滤波器)。
(3) 部件模版相对于根模版的空间位置。

首先要计算一个HOG金字塔：通过计算标准图像金字塔中每层图像的HOG特征得到HOG特征金字塔，HOG金字塔中每一层的的最小单位是细胞单元(cell)。

滤波器(模版)就是一个权重向量，一个$w \times h$大小的滤波器$F$是一个含$w \times h \times 9 \times 4$个权重的向量($9 \times 4$是一个HOG细胞单元的特征向量的维数)。所谓滤波器的得分就是此权重向量与HOG金字塔中$w \times h$大小子窗口的HOG特征向量的点积(DotProduct)。

而检测窗口的得分是根滤波器的分数加上各个部件的分数的总和，每个部件的分数是此部件的各个空间位置得分的最大值，每个部件的空间位置得分是部件在该子窗口上滤波器的得分减去变形花费。

假设$H$是HOG金字塔，$p = (x, y, l)$ 表示金字塔第$l$层 $(x, y)$ 位置的一个细胞单元。$ \phi (H, p, w, h)$是将金字塔$H$中以$p$为左上角点的$w \times h$大小子窗口的HOG特征串接起来得到的向量。所以，滤波器$F$在此检测窗口上的得分为：$F \cdot \phi (H, p, w, h)$。此后，在不引起歧义的情况下，我们使用$ \phi (H,p)$代表$ \phi (H, p, w, h)$。

所以，含$n$个部件的模型可以通过根滤波器$F_0$和一系列部件模型$(P_1,…, P_n)$来定义，其中$P_i = (F_i, v_i, s_i, a_i, b_i)$。$F_i$是第$i$个部件的滤波器；$v_i$和$s_i$都是二维向量，都以细胞单元为单位，$v_i$指明第$i$个部件位置的矩形中心点相对于根位置的坐标，$s_i$是此矩形的大小；$a_i$和$b_i$也都是二维向量，指明一个二次函数的参数，此二次函数用来对第$i$个部件的每个可能位置进行评分。

模型在HOG金字塔中的位置可以用$z = (p_0, ….. , p_n)$来表示，当$i=0$时，$p_i = (x_i, y_i, l_i)$表示根滤波器的位置；$i>0$时，$p_i = (x_i, y_i, l_i)$表示第$i$个部件滤波器的位置。我们假设每个部件所在层的HOG细胞单元的尺寸是根所在的层的细胞单元尺寸的一半。空间位置的得分等于每个部件滤波器的得分(从数据来看)加上(？加上减去都一样，通过正负号控制就行)每个部件的位置相对于根的得分(从空间来看)。
即：
$$
\begin{equation}
\sum_{i=0}^n F_i \cdot \phi (H, p_i) - \sum_{i=1}^n a_i \cdot ( \tilde{x_i}, \tilde{y_i}) + b_i \cdot ( \tilde{x_i}^2 , \tilde{y_i}^2 ) \tag{1}
\end{equation}
$$
公式(1)中左边表示所有滤波器(i从0开始，包括根滤波器和部件滤波器)的得分(即滤波器的权重向量与对应的HOG特征向量的点积)，右边表示所有部件滤波器(i从1开始)的形变花费。
其中：
$$
( \tilde{x_i}, \tilde{y_i} ) = \frac{(x_i,y_i) - [2(x_0,y_0) + v_i]}{s_i}
$$
其中$ ( \tilde{x_i}, \tilde{y_i} ) $表示部件$i$的变形程度，$\tilde{x_i}$和$\tilde{y_i}$在-1到1之间。
$(x_0,y_0)$是根滤波器在其所在层的坐标，为了统一到部件滤波器所在层需乘以2。
$v_i$是部件$i$相对于根的坐标偏移，所以$2(x_0, y_0)+v_i$表示未发生形变时部件$i$的坐标，
所以$(x_i,y_i) – [2(x_0,y_0) + v_i]$是部件$i$的形变位移量，再除以部件的矩形框大小$s_i$可保证在-1到1之间。
计算过程如下图：

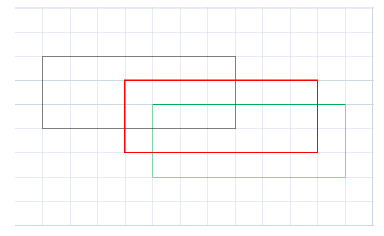
部件变形程度计算

图中每个格子表示部件所在HOG金字塔层的细胞单元，红框表示某部件未发生位移时的位置，部件大小为w=7,h=3
黑框表示部件的实际位置，因此
$ ( \tilde{x_i}, \tilde{y_i} ) = (-\frac{3}{7}, -\frac{1}{3}) $
同理，绿框所在位置对应：
$ ( \tilde{x_i}, \tilde{y_i} ) = (\frac{1}{7}, \frac{1}{3}) $

（2）在不完全标注(partially labeled)数据集上的学习

模型训练使用的数据集中只标注了整个目标的位置，没有标注出每个部件的位置，所以叫做部分标注或不完全标注，并不是说图片中有指定类别的目标没有标注出来，这里容易理解错误。
这种训练方法可以看做弱监督训练，正因为不知道目标中部件的位置，所以将部件的位置看做隐藏变量，使用LSVM进行训练，训练时同时估计部件位置和学习模型参数。

（3）半凸

LSVM最终是一个非凸规划(non-convex)问题。然而，在下面所讨论的情况下LSVM是半凸规划(semi-convexity)问题，一旦将隐藏信息指定给正样本则训练问题变为凸规划问题。

几个凸函数的最大值问题是凸规划问题。在线性SVM中，有$f_{\beta}(x) = \beta \cdot \Phi(x) $是$\beta$的线性函数，此时铰链损失函数对于每个样本都是凸的，因为它是两个凸函数的最大值。

注意到**公式(13)中定义的$f_{\beta}$是一系列函数的最大值，而这些函数都是$\beta$的线性函数，因此$f_{\beta}$是$\beta$的凸函数。所以当$y_i = -1$时，两个函数$f(x) = 0$和$f(x) = 1 - y_i f_{\beta}(x_i)$都是$\beta$的凸函数，所以铰链损失函数$max(0,1 - y_i f_{\beta}(x_i))$ 是$\beta$的凸函数。也就是说，只有当样本为负样本时，损失函数是$\beta$的凸函数。我们将损失函数的这一性质叫做半凸(semi-convexity)**。

对于正样本$(y_i= 1)$来说，LSVM的铰链损失函数不是凸函数，因为它是一个凸函数$ f(x)= 0 $和一个凹函数 $f(x) = 1 - y_i f_{\beta}(x_i)$ 的最大值。

但是，当LSVM的正样本的隐藏变量具有唯一可能的取值时，$f_{\beta}(x_i)$ 是$\beta$的线性函数，因此损失函数是$\beta$的凸函数，再加上半凸性质，**公式(14)**变为凸规划问题。

（4）坐标下降算法

对于含有隐藏变量的svm问题，使用坐标下降算法进行求解：
$$
\beta^*(D) = \mathop{argmin} \limits_{\beta} \lambda {||\beta||}^2 + \sum_{i=1}^n max(0, 1 - y_i f_{\beta}(x_i)) \tag{3}
$$

(1) 估计部件位置
保持$\beta$值不变，即将$\beta$看做常量，找到正样本的隐藏变量$z_i$的最优值：
$ z_i = argmax_{z \in Z(x_i)} \beta \cdot \Phi(x,z) $

(2) 学习模型参数
保持正样本的$z_i$值不变，即将$z_i$看做常量，通过解上面定义的凸规划问题(即标准SVM问题)最优化$\beta$值。

（5）难例挖掘定理

**定理1 设$C$是样本集$D$的一个子集，如果 $M(\beta^{\ast}(D),D) \subseteq C $ 则 $ \beta^{\ast}(C) = \beta^{\ast}(D) $ **
解释：在样本集$D$上训练一个分类器$\beta$( 即$\beta^{\ast}(D)$)，用$\beta$在样本集$D$上搜寻难例，得到难例集合即为$M(\beta^{\ast}(D),D)$，如果此难例集合包含于样本子集$C$，则在样本子集$C$上训练得到的分类器等价于在样本集$D$上训练得到的分类器。

定理2 若$ \beta^{\ast}(M(\beta,D)) = \beta $ 则 $ \beta = \beta^{\ast}(D) $
解释：现在有分类器$\beta$，$\beta$在样本集$D$上得到的难例集合为$M(\beta,D)$，用$M(\beta,D)$训练一个分类器，即为$\beta^{\ast}(M(\beta,D))$，如果训练出来的分类器等于$\beta$ (这说明什么呢？这说明初始分类器$\beta$已经足够好了，因为再加入难例进行训练得到的是和初始分类器相同的分类器)，则$\beta$就是样本集上的最优分类器。
迭代算法：
设$C$是最初的样本缓冲区(cache)。实际上可以将正样本和随机负样本放在一起。考虑如下迭代算法：

(1)设$\beta := \beta^{\ast}(C)$
(2)收缩$C$，使得$C := M(\beta,C)$
(3)通过不断向$C$中增加$M(\beta, D)$中的样本来增大$C$，直到达到内存限制L。

解释：

(1)$C$是一个样本缓冲区，在$C$上训练一个分类器$\beta$，即为$\beta^{\ast}(C)$。
(2)用$\beta$在$C$上搜寻得到的难例代替$C$，使$C$变小(收缩)。
(3)用$\beta$在原样本集$D$上搜索难例，得到难例集$M(\beta, D)$，从$M(\beta, D)$中拿出样本添加到$C$中，直到达到内存限制L。
重复步骤(1)，在$C$上训练一个新的分类器$\beta$，继续重复步骤(2)(3)。就这样不断重复步骤(1)(2)(3)，不断迭代。

定理3 如果每次经上述算法步骤2的迭代后，有$|C| < L$，则算法在有限时间内会收敛到$\beta = \beta^{\ast}(D)$。
解释：定理3是一个收敛条件，因为在定理2中迭代算法的第(3)步里会将样本缓冲区$C$增加到L大小，如果进行下一次迭代时，$C$可以变小，就说明算法在收敛。怎么理解呢？将分类器看做是一个学生，此学生在学习新知识，不断加入的新难例就是新知识，缓冲区$C$就是学生的书包，新加入的知识放到学生的书包中，如果每次学习过程书包变小，就说明学生将一些新加入的知识消化了，变成了学生的一部分。随着学习过程的进行，新知识一点一点被消化，学生也变得越来越聪明。在这里就是随着迭代过程的进行，难例被一点一点消化，分类器逐渐变得更好。

当前位置 : 首页 » 文章分类 : 科研 » 有关可变形部件模型(Deformable Part Model)的一些说明