以逻辑运算符 && 为例，对于 A && B 这个表达式，如果 A 表达式返回 false ，那么 A && B 已经确定为 false ，此时不会去执行表达式 B。
同理，对于逻辑运算符 ||，对于 A || B 这个表达式，如果 A 表达式返回 true ，那么 A || B 已经确定为 true ，此时不会去执行表达式 B。

下面这道题就利用到了逻辑运算的短路特性。
LeetCode.剑指offer.064.计算1到n的和

还有，比如三目运算符
boolean ret = condition ? isMatch() : false;
表示 condition 为 true 时结果是方法 isMatch() 的结果，否则是 false，可以简化为
condition && isMatch()

位运算

位运算 | 标签 - 小马的笔记

利用`a^a=0`消除元素

LeetCode.268.Missing Number 连续数组中缺失的数
 LeetCode.389.Find the Difference 找出两个数组的不同
 LeetCode.136.Single Number 数组中只出现一次的数

利用某bit位上的差异区分不同元素

LeetCode.137.Single Number II 数组中只出现一次的数2

LeetCode.260.Single Number III 数组中只出现一次的数3
LeetCode.剑指offer.056.数组中数字出现的次数

异或是无进位的加号

异或 ^ 被称为不进位的加号
左移 << 是一种进位或者乘法符号
公式：a + b = ( a ^ b ) + ( ( a & b ) << 1 )

LeetCode.371.Sum of Two Integers 不用加减号计算整数加法

-i等于i各位取反加1:`-i==~i+1`

i 为正数或负数时都成立

8的补码 0000 1000
-8的补码 1111 1000

90的补码 0101 1010
-90的补码 1010 0110

分离最右边的1:`i&(-i)`

求整数二进制表示中保留最低位1其余全为0对应的整数值
lowbit(i) 将i转化成二进制数之后，只保留最低位的1及其后面的0，截断前面的内容，然后再转成10进制数
则
1、lowbit(i) = i & -i;
证明：
将 i 的二进制表示写为 a1b，其中 b 是0个或多个0，也就是1是最低位的1
则 -i = ~i+1 = ~(a1b)+1 = (~a)0(~b) +1 = (~a)1b
则 i&-i = a1b & (~a)1b = 01b 也就是仅保留最低位1其余全是0的二进制对应的数

2、lowbit(i) = i - (i & (i-1));
将 i 的二进制表示写为 a1b，其中 b 是0个或多个0，也就是1是最低位的1
则 i-1 = a0(~b)
则 i & (i-1) = a1b & a0(~b) = a0b
则 i - (i & (i-1)) = a1b - a0b = 01b

LeetCode.260.Single Number III 数组中只出现一次的数3
LeetCode.剑指offer.056.数组中数字出现的次数

将最右边的1设为0:`x&(x-1)`

可用于统计整数的二进制表示中 1 的个数
x&(x-1) 可将 x 最右边的 1 设为 0，我们不断重复这个操作，直到x为0，就是1的个数

LeetCode.191.Number of 1 Bits 位1的个数

位运算技巧总结

判断一个整数是奇数还是偶数：将该数与 1 相与，结果为 0 则是偶数，结果为 1 则是奇数。
判断第 n 位是否是 1：x & (1<<n)，结果为 1 说明是，为 0 说明不是。
将第 n 位设为 1：y = x | (1<<n)
将第 n 为设为 0：y = x & ~(1<<n)
将第 n 位的值取反：y = x ^ (1<<n)
将最右边的 1 设为 0：y = x & (x-1)
分离最右边的 1：y = x & (-x)
将最右边的 1 后面都设位 1：y = x | (x-1)
分离最右边的 0：y = ~x & (x+1)
将最右边的 0 设为 1：y = x | (x+1)

你必须知道的基本位运算技巧
https://blog.whezh.com/bit-hacks/

循环左移/右移n位

循环右移就是依次将移出的低位放到该数的高位
循环左移就是依次讲移出的高位放到该数的低位

32位整数val循环左移n位 leftRotateN(val) = (val << n) | (val >>> (32-n))
32位整数val循环右移n位 rightRotateN(val) = (val >>> n) | (val << (32-n))
注意这里的右移一定是逻辑右移 >>> ，即右移左补0的右移，如果写成算术右移（符号右移） >> 就错了

不引入新变量交换两个数的值

加法

int a = a + b;
int b = a - b;
int a = a - b;

对于加减法实现的交换方法，有可能发生溢出。

异或

int a = a ^ b;
int b = a ^ b;
int a = a ^ b;

对于异或运算实现的交换方法，当 a=b 时结果为0

利用int的空闲bit位保存需要的信息

比如 input 数据取值范围是固定的，比如只有各位数，但使用了 int 类型，则肯定有空闲的bit位用不到，如果我们需要在原数据上保存一些计算得来的信息，可以使用这些空闲的比特位。
下面这个题就是典型的用空闲bit位保存信息
LeetCode.289.Game of Life 生命游戏

双指针

双指针 | 标签 - 小马的笔记

滑动窗口/快慢指针

滑动窗口 | 标签 - 小马的笔记

最长非重复子串 和 最小覆盖子串 是滑动窗口法的经典题目，学习滑动窗口一定要吃透。

使用滑动窗口必须回答的 3 个问题：
1、什么时候扩张右边界？滑动窗口内元素不满足条件时。
2、什么时候收缩左边界？找到一个满足条件的窗口后，开始收缩左边界，直到再次不满足条件。
3、什么时候更新目标值？当找到一个满足条件的窗口后，以及每次收缩滑动窗口左边界时。

LeetCode.076.Minimum Window Substring 最小覆盖子串
 LeetCode.003.Longest Substring Without Repeating Characters 最长非重复子串
 LeetCode.209.Minimum Size Subarray Sum 长度最小的子数组

slow/fast 快慢指针，slow 左边是要保留的元素
LeetCode.283.Move Zeroes 将数组中的零移到末尾
 LeetCode.027.Remove Element 从数组中移除指定元素
 LeetCode.026.Remove Duplicates from Sorted Array 删除有序数组中的重复项
 LeetCode.080.Remove Duplicates from Sorted Array II 删除有序数组中的重复项2

左右指针/前后指针

前后指针+交换

low/left 从前往后扫描，high/right 从后往前扫描

LeetCode.344.Reverse String 反转字符串
 LeetCode.541.Reverse String II 反转字符串 II

LeetCode.125.Valid Palindrome 验证回文串
 LeetCode.680.Valid Palindrome II 验证回文字符串 Ⅱ

LeetCode.027.Remove Element 从数组中移除指定元素

快速排序中的 partition 过程
给定无序数组，把奇数放到偶数之前（58同城中间件二面面试题）。

前后双指针根据条件向中间逼近

left/right 左右指针，两个指针根据条件逐渐向中间压缩来扫描
LeetCode.011.Container With Most Water 盛最多水的容器
 LeetCode.1013.Partition Array Into Three Parts With Equal Sum 将数组分成和相等的三个部分

排序+双指针

一些问题中，需要数组是有序的才方便移动指针，我们可以先将数组排序。
LeetCode.016.3Sum Closest 最接近的三数之和
 LeetCode.015.3Sum 三数之和
18 四数之和
https://leetcode-cn.com/problems/4sum/

两个数组(链表)中的双指针

LeetCode.392.Is Subsequence 判断是否子序列
 LeetCode.004.Median of Two Sorted Arrays 两个有序数组的中位数

给定两个整数数组a和b，计算具有最小差绝对值的一对数值（每个数组中取一个值），并返回该对数值的差
思路：
排序加双指针比较
O(nlog(n)) 快速排序，然后两个指针 a, b 分别从头到尾扫描，值小的往前走，过程中更新 min

面试题 16.06. 最小差
https://leetcode-cn.com/problems/smallest-difference-lcci/

倍速指针

2倍速指针，快指针是慢指针的2倍速
有环单链表的环长、环起点和链表长
 LeetCode.141.Linked List Cycle 判断链表是否有环
 LeetCode.142.Linked List Cycle II 有环链表的环起点

LeetCode.287.Find the Duplicate Number 数组中重复的数
 LeetCode.202.Happy Number 快乐数

链表中使用2倍速指针，找链表中点
LeetCode.876.Middle of the Linked List 链表的中间结点
 LeetCode.234.Palindrome Linked List 判断是否回文单链表

k间隔指针

k间隔指针，快指针比慢指针先走k步
LeetCode.061.Rotate List 旋转链表

LeetCode.092.Reverse Linked List II 反转链表的第m到n个结点

交替互换指针

两个指针分别指向两个链表，每个指针走到结尾后跳到另一个链表头部继续。
LeetCode.160.Intersection of Two Linked Lists 两链表的交点

二分搜索

二分搜索 | 标签 - 小马的笔记

二分搜索(Binary Search) 是一种在有序数组中查找某一特定元素的搜索算法
第一篇二分搜索论文在 1946 年发表，然而第一个没有 bug 的二分查找法却是在 1962 年才出现，中间用了 16 年的时间。

liweiwei的二分搜索模板讲解不错
https://github.com/ojeveryday/AlgoWiki

LeetCode.035.Search Insert Position 搜索插入位置
 LeetCode.034.Find First and Last Position of Element in Sorted Array 在排序数组中查找元素的第一个和最后一个位置

二分搜索计算mid的经典bug

int mid = (min + max) / 2;
这句代码在 min 和 max 很大的时候，会出现溢出的情况，从而导致数组访问出错。
正确的写法
int mid = min + (max - min) / 2;
或者，使用位运算无符号逻辑右移 1 位，注意：无符号位运算符的优先级较低，需要括号括起来
int mid = (low + high) >>> 1; JDK 中的写法
或者
int mid = min + ((max - min) >>> 1);

Java中的Arrays.binarySearch()的bug与修复

源码

public static int binarySearch(long[] a, long key) {
    return binarySearch0(a, 0, a.length, key);
}
private static int binarySearch0(long[] a, int fromIndex, int toIndex, long key) {
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        long midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

Java 语言中的二分搜索实现 Arrays.binarySearch() 起初也存在这个溢出 bug，这个 bug 存在了长达九年才被更正。
起初 JDK 中的错误写法是 int mid = (low + high) >> 1;
更正后改为 int mid = (low + high) >>> 1;

为什么改为无符号的逻辑右移后，就不会发生溢出了呢？
首先 low 和 high 都是正整数，最大可能取值是 Integer.MAX_VALUE，也就是二进制 0 后面 31 个 1
我们以最大值为例，Integer.MAX_VALUE + Integer.MAX_VALUE 两个整型最大值进行加法运算后还是会溢出为负值的
二进制为 11111111111111111111111111111110
但是，无符号右移一位后，由于最左边补的是0，又恢复为 Integer.MAX_VALUE 了，所以最终结果不会溢出，虽然中间结果还是溢出了，但最终结果是正确的。

分治法

分治 | 标签 - 小马的笔记

归并排序

数组中的逆序对

LeetCode.剑指offer.051.数组中的逆序对

合并K个排序链表

LeetCode.023.Merge k Sorted Lists 合并K个排序链表

148 排序链表
https://leetcode-cn.com/problems/sort-list/

315 计算右侧小于当前元素的个数

https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/

线段树

题中的分治法用到了线段树，但不是很好理解
LeetCode.053.Maximum Subarray 最大连续子序列和

回溯法

回溯 | 标签 - 小马的笔记

从全排列问题开始理解“回溯搜索”算法（深度优先遍历 + 状态重置 + 剪枝） - liweiwei
https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/

回溯法的代码模板DFS

回溯法一般使用深度优先搜索 DFS 递归在 决策树 上搜索来实现。
回溯法的代码套路是使用两个变量：
resultSet 结果集，存储所有可能的最终结果
path 或者 current 当前选择，保存已经走过的路径
每次做出选择后，把选择加入 path，dfs进行下次选择，完成后回退撤销当前选择（从path中删除选择）。
如果搜到一个状态满足题目要求（到达结束条件，或者到达决策树的叶子节点），就把 path 放到 resultSet 中。

算法框架：

List<T> resultSet;

void backtrack(List<T> path) {
  if (满足结束条件 || 到达决策树叶子节点) {
    // 把 path 加入结果集
    resultSet.add(path);
    return;
  }

  // 遍历选择列表
  for (选择 in 选择列表) {
    path = path + 选择; // 做选择
    backtrack(path); // 递归dfs搜索
    path = path - 选择; // 撤销选择
  }
}

一文学会回溯算法解题技巧
https://leetcode-cn.com/circle/article/DyPDtg/

回溯法中什么情况下需要回退(撤销选择)？

那么回溯法在 DFS 递归方法结束后，是否需要撤销刚才的选择呢？或者说需要重置状态，或者叫撤回选择？
其实很简单，具体分析使用的保存选择结果的数据结构
比如 Java 中使用集合类的引用，类似 List<>, Deque<> 则回退时需要把选择撤销掉，否则影响之后的结果，因为集合类的引用是方法栈之间共享的。
如果每次使用一个新的变量去保存选择结果，则不需要重置，比如每次 String + "当前选择" 新生成一个保存选择结果的 Stirng 到下一次 dfs 方法中，则递归完不需要要撤销，因为子调用中的结果不影响当前结果。

但是一般意义上的回溯，按照字面意思理解是只使用一个变量去搜索所有的状态空间，所以就有撤销选择的需要。
可以想象一根绳子，在深度优先遍历的过程中，变长变短（前进和回退），在恰当的地方（很多时候是在叶子结点）是我们需要的结果，这个时候需要做一个拷贝，把结果记录下来（加入结果集）。

排列组合

排列(Permutation)，是指从给定个数的元素中取出指定个数的元素进行排序。
组合(Combination)，是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

全排列(经典回溯模板)

全排列问题是一个非常经典的 回溯法 backtracking 应用，全排列的代码可以直接作为回溯法的代码模板，是非常值得一做的题目。

需要注意的地方：
1、满足结束条件或到达解空间叶子节点后，把当前选择加入结果集 resultSet 时，需要做一次拷贝，否则由于 Java 中的引用传递的是地址，后续操作会继续修改已经完成的选择，当然如果使用 String 则没有这个问题，使用其他集合类存储选择结果时都需要注意。
2、用 stack 存储当前选择，方便在末尾 push(选择) 和 pop(撤销)， LinkedList 实现了 Deque 接口，可当做栈使用。
3、我这里使用 Set 存储剩余可用选择，是一种很低效的浪费空间的做法，但方便理解，可以参考官方解法中的直接在原数组上用下标分隔已选和未选元素，并使用 Collections.swap 进行选择和撤销，或者，使用一个 boolean[] selected 数组标记是否选择过。

LeetCode.046.Permutations 全排列

可以参考 liweiwei 这个全排列的题解，以全排列问题为切入点，全面介绍了回溯法，很详细
从全排列问题开始理解「回溯」算法（深度优先遍历 + 状态重置 + 剪枝）
https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/

括号生成

LeetCode.022.Generate Parentheses 括号生成

78 子集(经典回溯模板)

快手一面面试题
滴滴国际一面面试题

https://leetcode-cn.com/problems/subsets/

贪心算法

贪心 | 标签 - 小马的笔记

贪心算法(Greedy Algorithm) 是指：在对问题求解时，总是做出在当前看来是最好的选择。也就是不从整体最优上加以考虑，贪心算法所做出决策是在某种意义上的局部最优解。

贪心策略适用的前提是：局部最优策略能导致产生全局最优解。
可以适用贪心的问题就是每一步局部最优，最后导致结果全局最优。

如何判断贪心算法是否适用？
1、直觉，根据直觉描述出来的算法，具备“只考虑当前，不考虑全局”的特点，那可能就是「贪心算法」；
2、如果不能举出反例，那多半这个问题就具有「贪心算法性质」，可以使用贪心算法去做。

经验：由于贪心算法适用的场景一般都是在一组决策里选择最大或者最小值，因此在使用贪心算法之前，经常需要先对数据按照某种规则排序。

贪心算法（Greedy Algorithm）是指：在对问题求解时，总是做出在当前看来是最好的选择。也就是不从整体最优上加以考虑，贪心算法所做出决策是在某种意义上的局部最优解。

LeetCode.056.Merge Intervals 合并重叠区间 - 题解 - liweiwei1419
https://leetcode-cn.com/problems/merge-intervals/solution/tan-xin-suan-fa-java-by-liweiwei1419-3/

跳跃游戏

LeetCode.055.Jump Game 跳跃游戏
 LeetCode.045.Jump Game II 跳跃游戏2

区间重叠问题

用最少数量的箭引爆气球

LeetCode.452.Minimum Number of Arrows to Burst Balloons 用最少数量的箭引爆气球

合并重叠区间

LeetCode.056.Merge Intervals 合并重叠区间

最大重叠区间数目

最大重叠区间数目 Maximum number of overlapping intervals

有一个party，许多人来参加。一个记录仪记录下了每个人到达的时间 s_i 和离开的时间 e_i ，也就是说每个人在party的时间为 [ s_i, t_i ]。求出这个party 同一时刻最多接纳了多少人。

例如：

Input: arrl  [] = {1, 2,  9, 5,  5}
       exit  [] = {4, 5, 12, 9, 12}
First guest in array arrives at 1 and leaves at 4, second guest arrives at 2 and leaves at 5, and so on.
Output: 5。There are maximum 3 guests at time 5.

解：
把所有的到达时间点 arrl 和所有离开时间点 exit 放一起从小到大排序，注意如果遇到到达时间和离开时间相同的，到达时间要放前面。
然后从小到大开始遍历，count 记录当前人数，遇到到达时间count加1，遇到离开时间count减1

最大重叠区间数目 Maximum number of overlapping intervals
https://blog.csdn.net/jiyanfeng1/article/details/46994235

区间最大重叠数
https://www.jianshu.com/p/3ca6574cf480

最大重叠区间大小

在一维坐标轴上有n个区间段，求重合区间最长的两个区间段。

解：
首先按照区间的左端点即start对n个区间段进行排序
从前往后扫描所有区间，每次求相邻两个区间的重叠区域，过程中更新最大重叠区间大小即可。

区间最大重叠
https://www.cnblogs.com/AndyJee/p/4732068.html

集合覆盖问题

已知猎头跟简历的对应关系，猎头手中的简历可能重叠，找到能获取全部简历的最少的猎头集合。
例如：

A -> 1 2 3 4
B -> 2 3 5
C -> 4 5 6
D -> 5 6 7 8
E -> 1 4 6
result: [A, D]

这题还有一种更常见的描述，广播台和城市（州）
每个广播台能覆盖一些城市，不同广播台覆盖的城市可能重合，求能覆盖所有城市的最小广播台集合。
例如：

广播台1 -> 北京 上海
广播台2 -> 天津 上海 武汉
广播台3 -> 北京 广州 深圳
广播台4 -> 北京 天津
广播台5 -> 深圳 上海

面试中还被问过另一种描述：
用户要买3个商品，每个商品若干个，现有多个商家，每个商家可提供的各个商品的个数如下：
商家1 -> (物品1, 3) (物品2, 2)
商家2 -> (物品2, 1) (物品3, 4)
商家3 -> (物品1, 1) (物品2, 2)
请问如何合理的选择商家？

1、暴力穷举法：
穷举所有可能的猎头组合，一共有 $ C_n^0 + C_n^1 + … + C_n^n = 2^n $ 种，即猎头集合的幂集，找到能覆盖所有简历集合的最小猎头集合个数。
时间复杂度 O(2^n * m) n是猎头数，m是猎头的平均简历数

2、贪心算法
设 coveredResumeSet 是已覆盖简历的集合，初始是空集。
headHunterSet 是已找到的猎头集合，初始为空集。
remainingHeadHunterSet 是剩余猎头集合，初始为全部猎头。

遍历剩余猎头集合 remainingHeadHunterSet, 每次找和已覆盖简历集合 coveredResumeSet 差集最大的猎头，将其加入已找到猎头集合 headHunterSet ，其简历加入 coveredResumeSet，将其从 remainingHeadHunterSet 删除。
不断循环遍历，一直到已覆盖集合 coveredResumeSet 是全部简历则结束。

java 代码如下

public class HeadHunterAndResume {
    public List<String> getLeastHeaderHunter(Map<String, List<Integer>> lt2jl) {
        if (null == lt2jl || lt2jl.size() == 0) {
            return Collections.emptyList();
        }
        // 所有简历全集
        Set<Integer> allResumeSet = new HashSet<>();
        lt2jl.forEach((k, list) -> allResumeSet.addAll(list));

        // 已覆盖的简历集合
        Set<Integer> coveredResumeSet = new HashSet<>();

        // 已找到的猎头集合
        Set<String> headHunterSet = new HashSet<>();
        // 剩余猎头集合
        Set<String> remainingHeadHunterSet = new HashSet<>(lt2jl.keySet());

        // 已覆盖集合为全集时结束
        while (coveredResumeSet.size() < allResumeSet.size()) {
            // 遍历剩余猎头集合 remainingHeadHunterSet, 每次找和已覆盖简历集合 coveredResumeSet 差集最大的猎头，将其加入已找到猎头集合 headHunterSet ，其简历加入 coveredResumeSet，将其从 remainingHeadHunterSet 删除
            int maxDiff = 0;
            String maxDiffHeaderHunter = "";
            for (String headHunter : remainingHeadHunterSet) {
                Set<Integer> resumeSet = new HashSet<>(lt2jl.get(headHunter));
                // resumeSet - coveredResumeSet 的差集
                Set<Integer> diffSet = difference(resumeSet, coveredResumeSet);
                if (diffSet.size() > maxDiff) {
                    maxDiff = diffSet.size();
                    maxDiffHeaderHunter = headHunter;
                }
            }
            remainingHeadHunterSet.remove(maxDiffHeaderHunter);
            headHunterSet.add(maxDiffHeaderHunter);
            coveredResumeSet.addAll(lt2jl.get(maxDiffHeaderHunter));
        }

        return new ArrayList<>(headHunterSet);
    }

    // 求 set1 - set2 的差集
    private <T> Set<T> difference(Set<T> set1, Set<T> set2) {
        if (null == set2 || set2.size() == 0) {
            return set1;
        }
        Set<T> resultSet = new HashSet<>(set1);
        for (T ele : set2) {
            resultSet.remove(ele);
        }
        return resultSet;
    }

    public static void main(String[] args) {
        HeadHunterAndResume headHunterAndResume = new HeadHunterAndResume();
        HashMap<String, List<Integer>> lt2jl = new HashMap<>();
        lt2jl.put("A", Arrays.asList(1,2,3,4));
        lt2jl.put("B", Arrays.asList(2,3,5));
        lt2jl.put("C", Arrays.asList(4,5,6));
        lt2jl.put("D", Arrays.asList(5,6,7,8));
        lt2jl.put("E", Arrays.asList(1,4,6));
        System.out.println(headHunterAndResume.getLeastHeaderHunter(lt2jl));
    }
}

《算法图解》第八章_贪婪算法_集合覆盖问题
https://www.cnblogs.com/OctoptusLian/p/9190176.html

贪心算法实践之集合覆盖问题
https://juejin.im/post/5da540a951882555a84305be

动态规划

动态规划 | 标签 - 小马的笔记

无后效性：某阶段的状态一旦确定，这个阶段以后的过程演变就和这个阶段以前的状态和决策无关了，只和这个阶段的状态有关，当前状态是此前历史的完整总结。
拿最长公共子序列 LCS 来说，你在后面碰到的字符不会影响你前面字符的匹配数量和结果，每次增加匹配到的字符时，都是“继承”前面的结果之后加一。
无后效性在随机过程中表述为 Markov 性质

最优子结构

斐波那契数列

509 Fibonacci Number
https://leetcode-cn.com/problems/fibonacci-number/

斐波那契数列第 n 项的计算方法：
LeetCode.070.Climbing Stairs 爬楼梯的官方题解最后总结了斐波那契数列的计算方法：
https://leetcode-cn.com/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/

1、递归计算，递归自顶向下计算，时间复杂度为 O(2^n)，有大量重复计算
2、动态规划，斐波那契数列的公式 f(n) = f(n-1) + f(n-2) 本身就是一个递推公式，可以自底向上计算，重复利用之前的计算结果，时间复杂度 O(n)，并利用滚动数组将空间复杂度降到 O(1)。
3、矩阵快速幂，时间复杂度 O(logn)
4、直接利用斐波那契数列第 n 项的通项公式计算，当然一般我们记不住这个公式。时间复杂度 O(logn)
$$
f(n) =
\frac{1}{\sqrt{5}}
\left[ \left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n \right]
$$

爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

dp[i] 表示爬 i 层台阶的方法数，则有递推公式 dp[i] = dp[i-1] + dp[i-2]
因为对于第 i 层台阶，我们可以从第 i-1 层台阶爬 1 层，或者从第 i-2 层台阶一次爬 2 层到达，所以爬 i-1 层台阶的方法数和爬 i-2 层台阶的方法数的总和就是爬 i 层台阶的方法数。
初始条件为 dp[0] = 1，dp[1] = 1

这个问题其实是一个斐波那契数列。

LeetCode.070.Climbing Stairs 爬楼梯

约瑟夫环

n 个人排成一个圆环，编号 0,1,…,n-1 ，从 1 开始报数，报到 m 的人退出，剩下的人继续从 1 开始报数。求最后胜利者的编号。

解：
设 f[n] 表示 n 个人组成的约瑟夫环中最后剩下人的编号，则有递推公式
$ f[n] = (f[n-1] + m) % n; n > 1 $
初始条件为：
$ f[1] = 0 $

LeetCode.剑指offer.062.圆圈中最后剩下的数字/约瑟夫环

最长公共子序列LCS

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列。
一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列，则返回 0。

注意区分最长公共子序列 Longest Common Substring 和最长公共子串 Longest Common Subsequence，子序列 Subsequence 不要求连续，子串 Substring 必须是连续的。

解：
设 lcs[i,j] 是序列 Xi=<x1, x2, …, xi> 和 Yj=<y1, y2, …, yj> 的最长公共子序列的长度，则有
$
lcs[i,j] =
\begin{cases}
0, & \text{if $i = 0$ or $j = 0$ } \\
cls[i-1, j-1] + 1, & \text{if $i,j > 0$ and $x_i = y_j$ } \\
max(cls[i-1][j], cls[i][j-1]), & \text{if $i,j > 0$ and $x_i \neq y_j$ }
\end{cases}
$

LeetCode.1143.Longest Common Subsequence 最长公共子序列LCS

最长公共子串LCS/最长重复子数组

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。
示例 1:

输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出: 3
解释:
长度最长的公共子数组是 [3, 2, 1]。

注意区分最长公共子序列 Longest Common Substring 和最长公共子串 Longest Common Subsequence，子序列 Subsequence 不要求连续，子串 Substring 必须是连续的。

解：
设 lcs[i,j] 是序列 Xi=<x1, x2, …, xi> 和 Yj=<y1, y2, …, yj> 的以 xi 和 yj 为结尾的(即必须包含xi和yj)最长公共子串的长度。
由于子串要求必须是连续的，其实也就是 xi,…,xm 和 yj,…,yn 的最长公共前缀。
所以，当 xi 和 yj 相等时，就能和前面的接上，以 xi 和 yj 为结尾的最长公共子串就是以 xi-1 和 yj-1 为结尾的最长公共子串的长度加1
当 xi 和 yj 不等时，以 xi 和 yj 为结尾的最长公共子串的长度就是0
对比
LeetCode.053.Maximum Subarray 最大连续子序列和
题，可以发现，当遇到连续子序列时，递推公式中一定是以xx为结尾的，因为只有这样才能和前面连续的接上。
或者可以这样对比子串和子序列：
由于子序列不连续，所以 dp[i][j] 可以从 dp[i-1][j] 或 dp[i][j-1] 转移过来，
由于子串必须连续，所以 dp[i][j] 只能从 dp[i-1][j-1] 转移。
而且，
子序列问题中，由于可以不连续，lcs[m][n] 就是最终结果。
但子串问题中，最终的结果并不是 lcs[m][n] ，而需要在递推的过程中不断更新最大值，也就是 lcs[0…m][0…n] 的最大值

所以
$
lcs[i,j] =
\begin{cases}
0, & \text{if $i = 0$ or $j = 0$ or $x_i \neq y_j$ } \\
cls[i-1, j-1] + 1, & \text{if $i,j > 0$ and $x_i = y_j$ } \\
\end{cases}
$

LeetCode.718.Maximum Length of Repeated Subarray 最长公共子串/最长重复子数组

最长有效括号子串

LeetCode.032.Longest Valid Parentheses 最长有效括号

最长上升子序列LIS

给定一个无序的整数数组，找到其中最长上升子序列的长度。
示例:

输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明: 可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。

解：
设 lis[i] 是 nums[0…i] 的最长上升子序列的长度，则

$ lis[i] = max(lis[j]) + 1, 0 \leq j \leq i-1 且 nums[j] < nums[i] $

从前往后求出所有 lis[0…n-1] ，其中的最大值就是真个数组 nums 的 lis

LeetCode.300.Longest Increasing Subsequence 最长上升子序列

最大连续子序列和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

设 dp[n] 是以 a[n] 为结尾的(必须包含a[n]在内)连续子序列的最大和，则有递推公式：
dp[n] = dp[n-1] + nums[n], dp[n-1] > 0
dp[n] = nums[n], dp[n-1] <= 0
或者 dp[n] = max(dp[n-1] + nums[n], nums[n])
因为
dp[n-1] > 0 时，加上 dp[n-1] 对 dp[n] 有增益作用。
dp[n-1] < 0 时, 加上 dp[n-1] 只会使 dp[n] 更小
初始条件为 dp[0] = nums[0]
从头到尾计算出 dp[0] 到 dp[n]，计算过程中出现过的最大 dp[i] 就是整个数组的最大连续子序列和

LeetCode.053.Maximum Subarray 最大连续子序列和

最大连续子序列积

给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。

设
max(i) 是 a[0,…,i] 中以 a[i] 为结尾的(必须包含a[i])连续子序列的乘积最大值
min(i) 是 a[0,…,i] 中以 a[i] 为结尾的(必须包含a[i])连续子序列的乘积最小值
由于乘积的负负得正特性，若 a[i] 是负值且 min(i-1) 也是负值，乘积可能诞生一个新的最大正值，这就是为什么我们还需要保存并不断更新一个乘积最小值。
可得递推公式：

$ max(i+1) = max(a[i+1], max(i) \times a[i+1], min(i) \times a[i+1]) $
$ min(i+1) = min(a[i+1], max(i) \times a[i+1], min(i) \times a[i+1]) $

从头到尾计算出 max(i) 和 min(i)，计算过程中出现过的最大 max(i) 就是整个数组的最大连续子序列积

LeetCode.152.Maximum Product Subarray 最大连续子序列积

最大非相邻子序列和(打家劫舍/按摩师)

给定一个整数数组 nums ，如果选择了 nums[i] 则 i 前后的两个数都不能再选择，也就是无法选择相邻的两个数，找出一个序列使得序列和最大。

解：
f[i] 表示 nums[0…i] 中非相邻子序列和的最大值，则对于第 i 个数来说有两种选择，选他或者不选他：
1、选 i 后就肯定不能选 i-1 ，可能获得的最大值为 f[i-2] + nums[i]
2、不选 i 则可以选择 i-1，可能获得的最大值为 f[i-1]
所以有递推公式：
f[i] = max(f[i-2] + nums[i], f[i-1])

初始条件为:
f[0] = nums[0]
f[1] = max(nums[0], nums[1])

LeetCode.198.House Robber 打家劫舍
 LeetCode.程序员面试金典.1716.Masseuse 按摩师

最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。

设 p(i,j) 表示子串 s[i,j] 是否回文串，若已知 s[i,j] 是否回文，则可轻松的知道左右各扩展一位的子串 s[i-1,j+1] 是否子串，所以有递推公式：
p[i-1,j+1] = p(i,j) && s[i-1] == s[j+1]
且有初始条件
p[i,i] = true
p[i,i+1] = s[i] == s[i+1]

填二维表的过程中，maxStr 记录当前得到的最长回文子串，每次得到一个 true 值时，比较是否比 maxStr 长度更长，如果是则更新 maxStr，填表结束后的 maxStr 就是最终结果。

LeetCode.005.LongestPalindromicSubstring 最长回文子串

零钱兑换-最少硬币数

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

解：
设 f(i) 是兑换金额 i 需要的最小零钱个数，硬币集合为 {c1, c2, …, cj} ，则有递推公式：
$
f(i) = \min_{j = 1…n} f(i - c_j) + 1
$

LeetCode.322.Coin Change 零钱兑换

零钱兑换-总方案数

给定数量不限的硬币，币值为25分、10分、5分和1分，编写代码计算n分有几种表示法。

LeetCode.程序员面试金典.0811.Coin 硬币

编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数。
你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符

解：
设 dist[i][j] 表示 word1[0...i-1] 转换为 word2[0...j-1] 的最小操作次数，也就是 word1 的前 i 个字符转换为 word2 的前 j 个字符需要的最小操作次数，则：
i == 0 时，表示 word1 是空串，则 dist[i][j] = j
j == 0 时，表示 word2 是空串，则 dist[i][j] = i
word1[i] == word2[j] 时， dist[i][j] = dist[i-1][j-1]
word1[i] != word2[j] 时， min(dist[i-1][j] + 1, dist[i][j-1] + 1, dist[i-1][j-1] + 1)

$ dist[i, j] =
\begin{cases}
j, & \text{ i == 0 } \\
i, & \text{ j == 0 } \\
dist[i-1, j-1], & \text{ word1[i] == word2[j] } \\
min(dist[i-1, j-1], dist[i-1][j], dist[i][j-1]) + 1, & \text{ word1[i] != word2[j] }
\end{cases}
$

LeetCode.072.Edit Distance 编辑距离

鸡蛋掉落问题

这道题太复杂了，动态规划的递推公式看了题解都非常难理解，然而直接写出来还会超时，必须用优化过的动态规划+二分搜索才能过。
具体解题过程看题解文章
LeetCode.887.Super Egg Drop 鸡蛋掉落
并结合 LeetCode 的官方题解及几个精选题解消化理解。

最大全1正方形

LeetCode.221.Maximal Square 最大正方形

最低票价

LeetCode.983.Minimum Cost For Tickets 最低票价

背包问题

崔添翼背包九讲最新版pdf
tianyicui / pack
https://github.com/tianyicui/pack

正则表达式匹配

LeetCode.010.Regular Expression Matching 正则表达式匹配
 LeetCode.044.Wildcard Matching 通配符匹配

单词拆分

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

设 dp[i] 表示 s 中前 i 个字符 s[0...i-1] 组成的子串是否可以拆分为单词
判断 s[0...i-1] 是否可拆分为单词时，我们只需遍历 0 <= j <= i-1 并判断 j 分隔的两个单词 s[0...j-1] 和 s[j...i-1] 是否分别可拆分为单词。其中，s[0...j-1] 是否可拆分为单词已记录在 dp[j] 中，只需判断 s[j...i-1] 是否是单词即可。
则有递推公式
dp[i] = dp[j] && dict.contains(s[j,i-1]), j = 0...i-1
初始条件 dp[0] = true，dp[s.length] 就是最终结果

LeetCode.139.Word Break 单词拆分

排序

LeetCode.912.Sort an Array 排序数组

快速排序(O(nlogn)不稳定)

快速排序的主要思想是通过划分将待排序的序列分成前后两部分，其中前一部分的数据都比后一部分的数据要小，然后再递归调用函数对两部分的序列分别进行快速排序，以此使整个序列达到有序。
具体来说，首先选取一个枢纽元（pivot），然后将数据划分成左右两部分，左边的大于（或等于）枢纽元，右边的小于(或等于枢纽元)，最后递归处理左右两部分。

步骤及实现

步骤：
1、选择枢轴
2、按枢轴分割
3、递归对左右两个子序列进行快速排序

按枢轴分割
改进的双向扫描
枢纽元保存在一个临时变量中，这样左端的位置可视为空闲。j从右向左扫描，直到A[j]小于等于枢纽元，检查i、j是否相交并将A[j]赋给空闲位置A[i]，这时A[j]变成空闲位置；i从左向右扫描，直到A[i]大于等于枢纽元，检查i、j是否相交并将A[i]赋给空闲位置A[j]，然后 A[i]变成空闲位置。重复上述过程，最后直到i、j相交跳出循环。最后把枢纽元放到空闲位置上。

代码实现

public class QuickSort {
    // 快速排序
    public static int[] sort(int[] nums) {
        if (null == nums || nums.length < 2) {
            return nums;
        }
        qsort(nums, 0, nums.length - 1);
        return nums;
    }

    // 递归对 nums[left,...,right] 进行快速排序
    private static void qsort(int[] nums, int left, int right) {
        if (left >= right) {
            return;
        }
        int location = partition(nums, left, right);  // 将数组分为两部分
        qsort(nums, left, location - 1); // 递归排序左子数组
        qsort(nums, location + 1, right); // 递归排序右子数组
    }

    // 进行一次partition，选nums[left]为枢轴，小于枢轴的放左边，大于枢轴的放右边，返回枢轴的位置
    private static int partition(int[] nums, int left, int right) {
        int pivot = nums[left]; // 选第一个数为枢轴
        while (left < right) {
            while (left < right && nums[right] >= pivot) {
                right--;
            }
            nums[left] = nums[right]; // 交换比枢轴小的记录到左端
            while (left < right && nums[left] <= pivot) {
                left++;
            }
            nums[right] = nums[left]; // 交换比枢轴小的记录到右端
        }
        // 枢轴归位
        nums[left] = pivot;
        return left; // 返回枢轴的位置
    }

    public static void main(String[] args) {
        System.out.println(Arrays.toString(QuickSort.sort(new int[] {4, 13, 2, 8, 1, 5, 1})));
        System.out.println(Arrays.toString(QuickSort.sort(new int[] {5,2,3,1})));
        System.out.println(Arrays.toString(QuickSort.sort(new int[] {5,1,1,2,0,0})));
        System.out.println(Arrays.toString(QuickSort.sort(new int[] {5,1})));
        System.out.println(Arrays.toString(QuickSort.sort(new int[] {1,5})));
        System.out.println(Arrays.toString(QuickSort.sort(new int[] {1,2,3,4,5})));
    }
}

时间复杂度

快速排序最佳运行时间 O(nlogn)，最坏运行时间 O(N^2)，随机化以后期望运行时间 O(nlogn)
空间复杂度 O(logn)，快速排序需要额外 O(logn) 的栈空间。

可以看出，每一次调用partition()方法都需要扫描一遍数组长度（注意，在递归的时候这个长度并不是原数组的长度n，而是被分隔出来的小数组，即n×(2^(-i))），其中i为调用深度。而在这一层同样长度的数组有2^i个。那么，每层排序大约需要O(n)复杂度。而一个长度为n的数组，调用深度最多为log(n)层。二者相乘，得到快速排序的平均复杂度为O(nlogn)。

通常，快速排序被认为是在所有同数量级的排序方法中，平均性能最好。

快速排序对数组中的数据分布很敏感，当数据分布较随机时，快速排序性能最好，复杂度为O(nlogn)，如果数组已基本有序，快排性能最差，复杂度为Ｏ(N^2)，退化为冒泡排序。

快速排序优化

优化枢轴选取

select_pivot(T A[], int p, int q)，该函数从A[p…q]中选取一个枢纽元并返回，且枢纽元放置在左端（A[p]的位置）。
固定选取：取序列的第一个元素为枢轴
随机选取：顾名思义就是从A[p…q]中随机选择一个枢纽元
三数取中：即取三个元素的中间数作为枢纽元，一般是取左端、右断和中间三个数，也可以随机选取。

LeetCode.912.Sort an Array 排序数组

分割到一定程度后使用插入排序

当待排序序列的长度分割到一定大小后，使用插入排序。
原因：对于很小和部分有序的数组，快排不如插排好。当待排序序列的长度分割到一定大小后，继续分割的效率比插入排序要差，此时可以使用插排而不是快排

if (high - low + 1 < 10) {
    InsertSort(arr,low,high);
    return;
}//else时，正常执行快排

递归栈优化(尾递归优化)

此外，快速排序需要一个递归栈，通常情况下这个栈不会很深，为log(n)级别。但是，如果每次划分的两个数组长度严重失衡，则为最坏情况，栈的深度将增加到O(n)。此时，由栈空间带来的空间复杂度不可忽略。如果加上额外变量的开销，这里甚至可能达到恐怖的O(n^2)空间复杂度。所以，快速排序的最差空间复杂度不是一个定值，甚至可能不在一个级别。

为了解决这个问题，我们可以在每次划分后比较两端的长度，并先对短的序列进行排序（目的是先结束这些栈以释放空间），可以将最大深度降回到O(㏒n)级别。

此外，快排函数在函数尾部有两次递归操作，我们可以对其使用尾递归优化
原因：如果待排序的序列划分极端不平衡，递归的深度将趋近于n，而栈的大小是很有限的，每次递归调用都会耗费一定的栈空间，函数的参数越多，每次递归耗费的空间也越多。优化后，可以缩减堆栈深度，由原来的O(n)缩减为O(logn)，将会提高性能。

private static void qsort(int[] arr, int low, int high){
    while (low < high) {
        int pivot = partition(arr, low, high);
        qsort(arr, low, pivot-1);
        low = pivot + 1;  //尾递归改为循环
    }
}

其实这种优化编译器会自己优化，相比不使用优化的方法，时间几乎没有减少

快速排序（简介、清晰）
https://www.cnblogs.com/codeskiller/p/6360870.html

三种快速排序以及快速排序的优化
http://blog.csdn.net/insistgogo/article/details/7785038

快速排序优化详细分析
http://blog.csdn.net/zuiaituantuan/article/details/5978009

快速排序应用

快速排序的应用主要是用到每次 partition 后枢轴的下标就是数组排序后的最终位置这一特性。

寻找第k大/小的数(找前k大/小的数)

输入n个整数，找出其中最小的k个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4。（剑指offer，面试题30，页数：167）
随机选取枢轴进行一次分割，得到分割后的枢轴位置loc，如果loc等于k，则找到第k小的数；如果loc大于k，继续在左边找；如果loc小于k，继续在右边找

平均时间复杂度 O(n)，最坏情况（数组已有序）下时间复杂度为 O(n^2)，空间复杂度 O(1)

LeetCode.215.Kth Largest Element in an Array 寻找数组中第K大的数
 LeetCode.剑指offer.040.数组中最小的k个数

求数组的众数/主元素(出现次数过半的数)

随机选取枢轴进行一次分割，得到分割后枢轴的位置loc，如果loc等于mid，则找到主元素；如果loc小于mid，在右边子序列中找主元素；如果loc大于mid，在左边子序列中找主元素。

其实用快速排序性质来找主元素比较麻烦，更好的方法是 摩尔投票算法，参考
LeetCode.169.Majority Element 数组的众数/主元素

//找出 arr 中 第  n/2  大的那个元素
public static int media_number(int[] arr){
    int left = 0;
    int right = arr.length - 1;
    int center = (left + right) / 2;

    int pivot_index = parition(arr, left, right);//枢轴元素的索引

    while(pivot_index != center)
    {
        if(pivot_index > center){
            right = pivot_index - 1;
            pivot_index = parition(arr, left, right);
        }
        else{
            left = pivot_index + 1;
            pivot_index = parition(arr, left, right);
        }
    }
    return arr[center];
}

快速排序及其应用
https://www.2cto.com/kf/201308/235343.html

堆排序(O(nlogn)不稳定)

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为 O(nlogn)，它也是不稳定排序。

如果一个数组 arr 中元素满足下面的关系时，称之为堆：
大顶堆：arr[i] >= arr[2i+1] 且 arr[i] >= arr[2i+2]
小顶堆：arr[i] <= arr[2i+1] 且 arr[i] <= arr[2i+2]

堆使用数组作为存储结构，但可以看做是一个完全二叉树，具有如下性质：
每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆(最大堆)；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆(最小堆)。

注意：堆中元素不是有序的，只能保证堆顶是最大、最小值。

堆排序的基本思想是(以升序排序为例)：
将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将堆顶和数组最后一个元素（下标 n-1 ）互换，从堆顶开始向下调整前 n-1 个元素再次成为大顶堆，堆顶是次大值，堆顶再和倒数第二个元素（下标 n-2 ）互换，再次调整前 n - 2 个元素为大顶堆，依次类推，直到堆中就剩一个元素，则排序完毕，数组成为一个升序序列。

一般升序采用大顶堆，降序采用小顶堆。

一次堆调整的时间复杂度是 O(logn)，所以堆排序的时间复杂度为 O(nlogn)

图解排序算法(三)之堆排序
https://www.cnblogs.com/chengxiao/p/6129630.html

TopK问题:寻找第(前)k大(小)的数

TopK | 标签

LeetCode.215.Kth Largest Element in an Array 寻找数组中第K大的数
 LeetCode.703.Kth Largest Element in a Stream 数据流中的第K大元素
 LeetCode.347.Top K Frequent Elements 前K个高频元素
 LeetCode.剑指offer.040.数组中最小的k个数
 LeetCode.023.Merge k Sorted Lists 合并K个排序链表

以找第 K 大的数为例，有两种方式：

容量为k的小顶堆(建议)

寻找第 k 大的数
建立一个长度为 K 的最小堆，用数组的前 K 个元素初始化，然后从第 K+1 个元素开始:
如果小于堆顶，由于堆顶是堆中最小的元素，小于堆顶就是小于堆中所有元素，所以不可能在前K大众，直接忽略，继续读入下一个
如果大于堆顶，压入堆中，O(logk) 调整堆，弹出堆顶。（或者先弹出堆顶，再压入当前元素。也就是先弹出堆顶还是后弹出都一样。）
这样最后最小堆里剩的就是最大的 K 个数，堆顶是第 K 大的数。

其实还可以简化这个过程：建立一个最小堆，原数组所有元素依次放入堆中，如果某次入堆后堆中元素个数大于 k，则弹出堆顶，也就是始终保持堆中元素个数小于等于 k，则最后堆顶就是第 k 大的数。

时间复杂度 O(nlogk)，空间复杂度 O(k)

容量为n的大顶堆(不建议)

维护一个容量为 n 的大顶堆(n是数组长度)，把所有元素依次放入堆中，最后把堆顶的 k-1 个元素弹出，也就是弹出前 k-1 大的数，则剩下的堆顶就是第 k 大值。
向大小为 n 的堆中添加元素的时间复杂度为 O(logn)，重复 n 次，故总时间复杂度为 O(nlogn)，空间复杂度 O(n)

所以，可以看出解决前(第)k大问题时，如果用最大堆，需要容量为数组长度的最大堆，当数据长度非常大时（比如几亿个数据中找top 10），空间开销非常大，所以不推荐用最大堆。
所以求前(第)k大，用最小堆，求前(第)k小，用最大堆。

为什么用最大堆解决前(第)k大问题时需要堆容量为n？

问：为什么用最大堆解决前(第)k大问题时需要堆容量为n（n为所有数据个数）？只用一个容量为k大最大堆不行吗？
答：堆中元素不是有序的，只能保证堆顶是最大值。如果想容量为k的大顶堆始终维持前k大个元素，则我们需要每次都找到这个k各元素中的最小值，将新加入值和他进行比较，而每次找最小值只能通过把堆顶依次poll掉剩最后一个元素来实现，代价非常大。复杂度为 O(nklogk)

归并排序(O(nlogn)稳定)

归并排序(Merge Sort) 是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略

归并排序将待排序数组A[1..n]分成两个各含n/2个元素的子序列，然后对这个两个子序列进行递归排序，最后将这两个已排序的子序列进行合并，即得到最终排好序的序列。

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

因为归并排序每次都是在相邻的数据中进行操作，所以归并排序在O(NlogN)的几种排序方法（快速排序，归并排序，希尔排序，堆排序）也是效率比较高的。

public static int[] sort(int[] nums) {
    return mergeSort(nums, 0, nums.length - 1);
}

private static int[] mergeSort(int[] nums, int start, int end) {
    if (start == end) {
        return new int[] {nums[start]};
    }
    int mid = (start + end) / 2;
    int[] leftNums = mergeSort(nums, start, mid);
    int[] rightNums = mergeSort(nums, mid + 1, end);
    int[] merge = new int[end - start + 1];
    int i = 0, j = 0, k = 0;
    while (i < leftNums.length && j < rightNums.length) {
        // 注意，这里必须是小于等于，如果写成小于，则归并排序就是不稳定的了
        if (leftNums[i] <= rightNums[j]) {
            merge[k++] = leftNums[i++];
        } else {
            merge[k++] = rightNums[j++];
        }
    }
    while (i < leftNums.length) {
        merge[k++] = leftNums[i++];
    }
    while (j < rightNums.length) {
        merge[k++] = rightNums[j++];
    }
    return merge;
}

图解排序算法(四)之归并排序
http://www.cnblogs.com/chengxiao/p/6194356.html

白话经典算法系列之五归并排序的实现（讲的真好）
https://blog.csdn.net/yuehailin/article/details/68961304

排序算法（2）——归并排序
https://blog.csdn.net/tmylzq187/article/details/51816084

数组中的逆序对

LeetCode.剑指offer.051.数组中的逆序对

Timsort(归并加插入)(O(nlogn)稳定)

TimSort 排序算法是 Python 和 Java 针对对象数组的默认排序算法。
TimSort排序算法的本质是归并排序算法，只是在归并排序算法上进行了大量的优化。对于日常生活中我们需要排序的数据通常不是完全随机的，而是部分有序的，或者部分逆序的，所以TimSort充分利用已有序的部分进行归并排序。

TimSort算法的核心在于利用数列中的部分有序。

Timsort是结合了归并排序（merge sort）和插入排序（insertion sort）而得出的排序算法，它在现实中有很好的效率。
Tim Peters在2002年设计了该算法并在Python中使用（TimSort 是 Python 中 list.sort 的默认实现）。该算法找到数据中已经排好序的块-分区，每一个分区叫一个run，然后按规则合并这些run。Pyhton自从2.3版以来一直采用Timsort算法排序，现在Java SE7和Android也采用Timsort算法对数组排序。

Timsort排序算法中定义数组中的有序片段为run，每个run都要求单调递增或严格单调递减（保证算法的稳定性）

TimSort 算法为了减少对升序部分的回溯和对降序部分的性能倒退，将输入按其升序和降序特点进行了分区。排序的输入的单位不是一个个单独的数字，而是一个个的块-分区。其中每一个分区叫一个run。针对这些 run 序列，每次拿一个 run 出来按规则进行合并。每次合并会将两个 run合并成一个 run。合并的结果保存到栈中。合并直到消耗掉所有的 run，这时将栈上剩余的 run合并到只剩一个 run 为止。这时这个仅剩的 run 便是排好序的结果。

综上述过程，Timsort算法的过程包括
（0）如何数组长度小于某个值，直接用二分插入排序算法
（1）把待排数组划分成一个个run
（2）将run入栈，任何时刻，当栈顶的 run 的长度不满足下列约束条件中任意一个时，
runLen[n-2] > runLen[n-1] + runLen[n], 即栈顶2个run的长度之和要小于第3个run
runLen[n-1] > runLen[n], 即栈顶run的长度要小于第二个run的长度
则利用归并排序将其中最短的2个run合并成一个新run，最终栈空的时候排序也就完成了。

为什么要有这两个奇怪的约束条件呢？每次入栈的时候直接进行归并不行吗？
这主要是考虑到归并排序的效率问题，因为将一个长序列和一个短序列进行归并排序从效率和代价的角度来看是不划算的，而两个长度均衡的序列进行归并排序时才是比较合理的也比较高效的。

run是已经排好序的一块分区。run可能会有不同的长度，每个run最少要有2个元素。Timesort根据run的长度来选择排序的策略。例如如果run的长度小于某一个值，则会选择插入排序算法来排序。

Timesor按照升序和降序划分出各个run：

run如果是是升序的，那么run中的后一元素要大于或等于前一元素；
如果run是严格降序的，即run中的前一元素大于后一元素，需要将run 中的元素翻转（这里注意降序的部分必须是“严格”降序才能进行翻转。因为 TimSort 的一个重要目标是保持稳定性stability。如果在 >= 的情况下进行翻转这个算法就不再是 stable）。

JDK中Timsort的Bug

TimSort 中是根据输入数组的长度申请固定大小的栈的
ComparableTimSort 类中

int stackLen = (len <    120  ?  5 :
                    len <   1542  ? 10 :
                    len < 119151  ? 24 : 49);

其中len表示输入的Array的长度，stackLen表示申请的栈的大小。

当栈内的所有 run 都满足
runLen[n-2] > runLen[n-1] + runLen[n], 即栈顶2个run的长度之和要小于第3个run
runLen[n-1] > runLen[n], 即栈顶run的长度要小于第二个run的长度
这个合并的条件时，排序过程中栈是不会溢出的，总是够用。
但是，TimSort 的实现不能保证站内所有run的长度都满足这两个条件，只能保证栈顶的3个元素满足，所以会出现该merge而没merge的run占用栈空间导致栈溢出，也就是数组下标溢出 ArrayIndexOutOfBoundsException

形式化方法的逆袭——如何找出Timsort算法和玉兔月球车中的Bug？
https://bindog.github.io/blog/2015/03/30/use-formal-method-to-find-the-bug-in-timsort-and-lunar-rover/

Timsort原理介绍
https://blog.csdn.net/yangzhongblog/article/details/8184707

简易版的TimSort排序算法
https://www.cnblogs.com/nullzx/p/6014471.html

深入理解 timsort 算法（1）：自适应归并排序
http://blog.jobbole.com/99681/

冒泡排序(O(n^2)稳定)

冒泡排序是从左到右依次比较相邻的两个元素，如果前一个元素比较大，就把前一个元素和后一个交换位置，遍历数组之后保证最后一个元素相对于前面的永远是最大的。然后让最后一个保持不变，重新遍历前n-1个元素，保证第n-1个元素在前n-1个元素里面是最大的。依此规律直到第2个元素是前2个元素里面最大的，排序就结束了。

时间复杂度 O(n^2)，空间复杂度 O(1)

冒泡算法是稳定的，在冒泡的过程中如果两个元素相等，那么他们的位置是不会交换的。

选择排序(O(n^2)不稳定)

选择排序的思路比较简单，先找到前n个元素中最大的值，然后和最后一个元素交换，这样保证最后一个元素一定是最大的，然后找到前n-1个元素中的最大值，和第n-1个元素进行交换，然后找到前n-2个元素中最大值，和第n-2个元素交换，依次类推到第2个元素，这样就得到了最后的排序数组。

其实整个过程和冒泡排序差不多，都是要找到最大的元素放到最后，不同点是冒泡排序是不停的交换元素，而选择排序只需要在每一轮交换一次。

时间复杂度 O(n^2)，空间复杂度 O(1)

选择排序最简单的版本是不稳定的，比如数组[1,3,2,2]，表示为[1,3,2(a),2(b)]，在经过一轮遍历之后变成了[1,2(b),2(a),3]，两个2之间的顺序因为第一个2和3的调换而颠倒了，所以不是稳定排序。

插入排序(O(n^2)稳定)

插入排序的核心思想是遍历整个数组，保持当前元素左侧始终是排序后的数组，然后将当前元素插入到前面排序完成的数组的对应的位置，使其保持排序状态。

时间复杂度 O(n^2)，空间复杂度 O(1)

插入排序是稳定排序，每次交换都是相邻元素的交换，不会有选择排序的那种跳跃式交换元素。

希尔排序(减少插入排序的移动次数)

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

希尔排序在数组中采用跳跃式分组的策略，通过某个增量将数组元素划分为若干组，然后分组进行插入排序，随后逐步缩小增量，继续按组进行插入排序操作，直至增量为1。希尔排序通过这种策略使得整个数组在初始阶段达到从宏观上看基本有序，小的基本在前，大的基本在后。然后缩小增量，到增量为1时，其实多数情况下只需微调即可，不会涉及过多的数据移动。

希尔排序中对于增量序列的选择十分重要，直接影响到希尔排序的性能。我们上面选择的增量序列{n/2,(n/2)/2…1}(希尔增量)，其最坏时间复杂度依然为O(n2)，一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为O(n3/2)。

希尔排序可以减少插入排序的移动次数。

在实际使用中，其时间复杂度仍然是一个悬而未决的问题，基本在 O(n^2) 和 O(n^{4/3}) 之间。

空间复杂度是 O(1)，是原地算法。

这个算法是不稳定的，里面有很多不相邻元素的交换操作。

图解排序算法(二)之希尔排序
https://www.cnblogs.com/chengxiao/p/6104371.html

珠排序(Bead Sort)

珠排序只能用于正整数排序。

珠排序中，正整数 n 用 n 个排成一行的珠子来表示。
一行（row）表示一个数字。如果一行里有2颗珠子，该行代表数字2；如果一行里有4颗珠子，该行代表数字4。当给定一个数组，数组里有多少个数字，就要有多少行；
数组里最大的数字是几，就要准备多少根杆子。

准备就绪后，释放珠子，珠子按重力下落，就完成了排序。

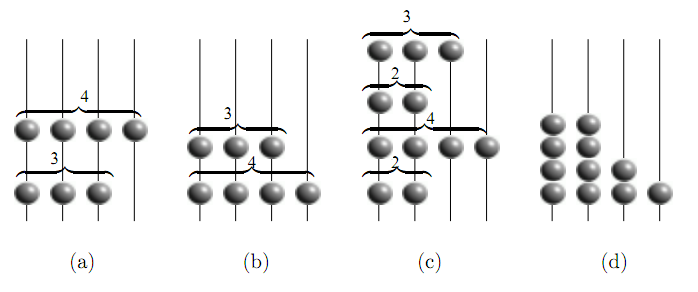
跳跃表

(a) 中有两个数字,4和3,分别串在四条线上, 于是数字4的最后一个珠子下落,因为它下边是空的,自由下落后变成(b)
(c) 中随机给了四个数字,分别是3,2,4,2, 这些珠子自由下落,就变成了(d)中,落完就有序了,2,2,3,4

计数排序(O(n)稳定)

计数排序是一个最基本的非比较排序，能够将时间复杂度提高到 O(n) 的水平，但是使用上比较有局限性，通常只能应用在键的变化范围比较小的情况下，如果键的变化范围特别大，建议使用基数排序。

计数排序的过程是创建一个长度为数组中最小和最大元素之差的数组，分别对应数组中的每个元素，然后用这个新的数组来统计每个元素出现的频率，然后遍历新的数组，根据每个元素出现的频率把元素放回到老的数组中，得到已经排好序的数组。

private void countSort(int[] nums) {
    int min = Integer.MAX_VALUE;
    int max = Integer.MIN_VALUE;
    for (int num : nums) {            // 找到最大最小值
        min = Math.min(min, num);
        max = Math.max(max, num);
    }
    int[] count = new int[max-min+1]; // 建立新数组
    for (int num : nums) {            // 统计每个元素出现频率
        count[num-min]++;
    }
    int cur = 0;
    for (int i = 0; i < count.length; i++) {  // 根据出现频率把计数数组中的元素放回到旧数组中
        while (count[i]>0) {
            nums[cur++] = i+min;
            count[i]--;
        }
    }
}

计数排序能够将时间复杂度降低到 O(n+r)（r为数组元素变化范围），不过这是对于数组元素的变化范围不是特别大。随着范围的变大，计数排序的性能就会逐渐降低。

空间复杂度为 O(n+r) ，随着数组元素变化范围的增大，空间复杂度也会变大。

计数排序是稳定的，原来排在前面的相同在计数的时候，仍然是排在每个计数位置的前面，在最后复原的时候也是从每个计数位的前面开始复原，所以最后相对位置还是相同的。

十二种排序算法包你满意（带GIF图解）
https://leetcode-cn.com/problems/sort-an-array/solution/shi-er-chong-pai-xu-suan-fa-bao-ni-man-yi-dai-gift/

桶排序(Bucket Sort)(O(n)稳定)

桶排序是将所有的元素分布到一系列的区间（也可以称之为桶）里面，然后对每个桶里面的所有元素分别进行排序的算法。

首先新建一个桶的数组，每个桶的规则需要提前制定好，比如元素在0~~9为一个桶、10~~19为一个桶。然后遍历整个待排序的数组，把元素分配到对应的桶里面。接下来单独对每个桶里面的元素进行排序，排序算法可以选择比较排序或者非比较排序，得到排序后的数组。最后把所有的桶内的元素还原到原数组里面得到最后的排序数组。

时间复杂度上桶排序和计数排序一样，是 O(n+r) 的水平，但是随着数据元素范围的增大，时间消耗也在增大。

空间复杂度也是 O(n+r)，需要额外的空间来保存所有的桶和桶里面的元素。

桶排序是稳定的（前提是桶内排序的逻辑是稳定的），和计数排序的逻辑类似，遍历过程插入桶的过程中没有改变相同元素的相对位置，排序也没有改变，最后的还原也没有改变。

基数排序(Radix Sort)(O(dn)稳定)

基数排序只能用于整数排序。

基数排序和桶排序有点相似，基数排序中需要把元素送入对应的桶中，不过规则是根据所有数字的某一位上面的数字来分类。

假设当前数组的所有元素都是正数，桶的数量就固定在了10个，然后计算出最大元素的位数。首先根据每个元素的最低位进行分组，比如1就放入1这个桶，13就放入3这个桶，111也放入1这个桶，然后把所有的数字根据桶的顺序取出来，依次还原到原数组里面。在第二轮从第二位开始分组，比如1（看作01）放入0这个桶，13放入1这个桶，111也放入1这个桶，再把所有的元素从桶里面依次取出放入原数组。经过最大元素位数次的这样的操作之后，还原得到的数组就是一个已经排好序的数组。

时间复杂度 O(N*d), N 为元素个数，d 为数字长度。
空间复杂度 O(N)

基数排序是一个稳定排序算法，在排序添加元素的过程中没有改变相同元素的相互位置。

摊还分析

摊还分析不同于平均情况分析，它并不涉及不同输入出现的概率，可以保证最坏情况下每个操作的平均性能。这样，就可以说明一个操作的平均代价是很低的，即使序列中某个单一操作的代价很高。

摊还分析
https://blog.csdn.net/zhongkelee/article/details/44563355

圈复杂度

圈复杂度用来衡量一个模块判定结构的复杂程度，数量上表现为线性无关的路径条数，即合理的预防错误所需测试的最少路径条数。圈复杂度大说明程序代码可能质量低且难于测试和维护

如果一段源码中不包含控制流语句（条件或决策点），那么这段代码的圈复杂度为1，因为这段代码中只会有一条路径；如果一段代码中仅包含一个if语句，且if语句仅有一个条件，那么这段代码的圈复杂度为2；包含两个嵌套的if语句，或是一个if语句有两个条件的代码块的圈复杂度为3。

NP问题与NPC问题

归并排序的时间复杂度是 O(nlogn)
冒泡排序的时间复杂度是 O(n^2)
Floyd算法的时间复杂度是 O(n^3)
尽管这些算法的运行时间有数量级上的差别，但是它们的时间复杂度都可以用 O(n^k) 来表示，k是一个常数。
因此，这些算法都是多项式时间算法，能用多项式时间算法解决的问题被称为P问题(Polynomial)

有些算法的时间复杂度是 O(2^n) 或 O(n!)，这类非多项式时间复杂度的算法被称为 NP(Non-deterministic Polynomial) 问题

有些科学家认为，所有的NP问题终究都可以在多项式时间内解决，只是我们暂时还没有找到方法；也有些科学家认为，某些NP问题永远无法在多项式时间内解决。
这个业界争论可以用一个公式来表达：
NP = P?

在NP问题之间，也可以存在归约关系。我们把众多的NP问题层层归约，必定会得到一个或多个“终极问题”，这些归约的终点就是所谓的 NPC问题(NP-complete) 即 NP完全问题。

旅行商问题TSP

旅行推销员问题(Travelling Salesman Problem, TSP)
一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，经过所有城市一次且仅一次后回到出发地。应如何选择行进路线，以使总的行程最短。

从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的哈密尔顿回路。

复杂度
从初始点出发的周游路线一共有(n-1)!条，即等于除初始结点外的n-1个结点的排列数，因此旅行商问题是一个排列问题。通过枚举(n-1)!条周游路线，从中找出一条具有最小成本的周游路线的算法，时间复杂度为 O(n!)
TSP问题是NP完全问题。

求解
对于规模较小的TSP问题，可以使用动态规划求解，对于规模较大的TSP问题，可使用贪心算法等求近似解。

应用
一开始是为交通运输而提出的，比如飞机航线安排、送邮件、快递服务、设计校车行进路线等等。实际上其应用范围扩展到了许多其他领域。

漫画：什么是旅行商问题？ - 程序员小灰
https://blog.csdn.net/bjweimengshu/article/details/100074636

哈密尔顿回路

哈密顿路径问题在上世纪七十年代初，终于被证明是“NP完全”的。

图着色问题

图着色问题（Graph Coloring Problem, GCP）又称着色问题，是最著名的NP-完全问题之一。

图的m可着色判定问题
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。

图的m可着色优化问题
若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。

求解
1、贪心
图的m色优化算法可用贪心法来解，其思想是：
任选一顶点着色1，在图中尽可能多的用颜色1着色；
当不能用颜色1着色时，转用颜色2将未着色的顶点尽可能多的着色···
直到所有顶点都被着色停止。

m-图着色问题（贪心解法）
https://blog.csdn.net/lime1991/article/details/47805881

2、DFS深度优先搜索
对于当前的节点cur，其前面的节点已经着色过了，判断cur节点可以使用的颜色即可。如何判断cur节点可以使用的颜色呢？遍历所有颜色，判断当前颜色i和cur周围节点的颜色是不是不一样，如果是的话，那么可行；否则，不可行。

应用
着色问题可以用来解 有冲突的资源安排问题
对于一项工程，用顶点表示工作，如果两项工作不能同时进行就用一条边连接对应的顶点。工作的资源安排对应这个图的点的着色：着同一种颜色的顶点对应的工作可以安排同样的资源进行，所需的最少资源就是这个图着色所需的最少颜色数。

例1 会议安排问题
学校的学生会下设6个部门，部门的成员如下：
部门1 -> {张，李，王}
部门2 -> {李，赵，刘}
部门3 -> {张，刘，王}
部门4 -> {赵，刘，孙}
部门5 -> {张，王}
部门6 -> {李，刘，王}
每个月每个部门都要开一次会，为了确保每个人都能参加他所在部门的会议，这6个会议至少需要安排在几个不同的时间段？
解：
用顶点 v1,v2…v6 分别代表部门1，部门2…部门6，2个顶点之间有一条边当且仅当它们代表的委员会成员中有共同的人，也就是不能同时进行，然后给此图着色，相邻顶点不同色的最小着色数就是需要的最小时间段数。

例2 频道分配问题
有5台设备，要给每一台设备分配一个波长。如果两台设备靠得太近，则不能给它们分配相同的波长，以防干扰。已知v1和v2，v1和v4，v2和v4，v3跟v4靠得太近。问至少需要几个发射波长。
解：
以设备为顶点构造一个图，如果两台设备靠得太近，则用一条边连接它们。于是，这个这个图的着色给出一个波长分配方案：给着同一种颜色的设备同一个波长。需要的最小颜色数就是最小波长数。

例3 考场安排问题
设学校共有n门课，需要进行期末考试，因为不少学生不止选修一门课程，所以不能把同一个学生选修的两门课程安排在同一场次进行考试，问学期的期末考试最少需多少场次考完？
解：
将所选的每门课程变成一个结点，如果两门课程的选课学生中有相同的学生，则用一条边连接这两门课，表示不能同时进行。则相邻边的顶点不能着同一种颜色，既不能安排在同一场次考试。最小着色数就是需要的最小场次数。

尾递归优化(改为循环)

与普通递归相比，由于尾递归的调用处于方法的最后，因此方法之前所积累下的各种状态对于递归调用结果已经没有任何意义，因此完全可以把本次方法中留在堆栈中的数据完全清除，把空间让给最后的递归调用。这样的优化便使得递归不会在调用堆栈上产生堆积，意味着即时是“无限”递归也不会让堆栈溢出。这便是尾递归的优势。
尾递归：http://www.cnblogs.com/JeffreyZhao/archive/2009/04/01/tail-recursion-explanation.html

数据结构

数组

抽屉原理/鸽巢原理

抽屉原理/鸽巢原理，即“一个萝卜一个坑”，十个萝卜放到9个坑里，肯定有一个坑里有2个萝卜。

原理1：把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。
原理2：把多于mn(m乘n)+1（n不为0）个的物体放到n个抽屉里，则至少有一个抽屉里有不少于（m+1）的物体。
原理3：把（mn－1）个物体放入n个抽屉中，其中必有一个抽屉中至多有（m—1）个物体

LeetCode.442.Find All Duplicates in an Array 数组中所有重复的数

数组下标哈希

`1 ≤ a[i] ≤ n`值在下标范围内

一看到题干中有 1 ≤ a[i] ≤ n，立即就要想到是用数组下标技巧做。
数组下标原地哈希法，在输入数组本身以某种方式标记已访问过的数字，用下标a[i]处的值a[a[i]]标记数值a[i]是否出现过。
但是下标 a[i] 上原有的值不能被覆盖，那怎么办呢？
由于数组中所有元素值都是正数，可以将元素值取反来标记此下标对应的值位出现过。
即对于数据中的每个值 a[i] ，将值 a[a[i]] 取反来表示这个值出现过，利用原数组空间的同时还不覆盖原数组的值（通过取绝对值可得原值）。。
这样做的好处是不需要额外的空间，空间复杂度为 O(1)

下面是非常典型的3个题：
1、遍历过程中遇到已经是负值的对应的下标是出现过的重复的数
LeetCode.442.Find All Duplicates in an Array 数组中所有重复的数

2、遍历一遍后没有被取反的元素对应的下标是缺失的数
LeetCode.448.Find All Numbers Disappeared in an Array 数组中消失的数

无法直接进行数组下标哈希，要先对原数组的数据进行处理
LeetCode.041.First Missing Positive 数组中缺失的第一个正数

3、即求重复的，又求缺失的
LeetCode.645.Set Mismatch 找出数组中重复的数和缺失的数

`'a' ≤ a[i] ≤ 'z'`值只包含大小写字母

遇到有提示仅包含小写（或者大写）英文字母的题，都可以尝试构造长度为26的数组作为map 比如

int[26] for Letters ‘a’ - ‘z’ or ‘A’ - ‘Z’
int[128] for ASCII
int[256] for Extended ASCII

LeetCode.389.Find the Difference 找出两个数组的不同
 LeetCode.1160.Find Words That Can Be Formed by Characters 拼写单词
 LeetCode.409.Longest Palindrome 最长回文串

还有比如题目中规定了数组元素 a[i] 的界限，比如都是 100 之内的数，也可以使用长度为 100 的数组来做map int[] map = new int[100];

LeetCode.575.Distribute Candies 分糖果

滚动数组

滚动数组是一种节约空间复杂度的数组压缩方法，假如数组的当前项 nums[i] 只依赖于前一个值 nums[i-1] 或固定的前几个值，则我们只需要几个变量来保存这些被依赖值，并滚动更新，而不需要保存整个数组。

一维数组压缩为1个或多个变量

滚动数组经常用于动态规划中的填表优化，比如：
1、最大子序列和的递归公式 dp[i] = max(dp[i-1] + nums[i], nums[i]) 中，可以使用一个变量 pre 保存前一个 dp 值并滚动更新，并不需要初始化一个 dp 数组。
2、计算斐波那契数列时，有公式 f(x) = f(x-1) + f(x-2)，我们可以用变量 prePre 保存 f(x-2) 的值，用变量 pre 保存 f(x-1) 的值，并滚动更新。

LeetCode.053.Maximum Subarray 最大连续子序列和
 LeetCode.837.New 21 Game 新21点
 LeetCode.070.Climbing Stairs 爬楼梯

二维数组压缩为1个或多个一维数组

滚动数组思想也可用于二维数组，可以将二维数组压缩为 1 个或多个一维数组。

LeetCode.097.Interleaving String 交错字符串

数组形式的链表

把数组看做链表，即把下标 i 处的值 a[i] 看做 next 指针，也就是每个元素的值是下一个链表节点的地址，则数组转化为链表。
LeetCode.287.Find the Duplicate Number 数组中重复的数

子数组(序列/串)的3种遍历方式

通常我们遍历子串/子序列/子数组有三种方式，都是 O(n^2) 复杂度

固定起始下标
固定结束下标
固定子数组长度

别小看这三种暴力枚举遍历方式，只有对这三种方式非常熟悉，才能根据题意进一步优化出 O(n) 的解法。

以数组 [1, 2, 3] 为例

固定起始下标

固定起始下标，首先遍历以 1 开头的子数组 [1]，[1, 2]，[1, 2, 3], 再遍历以 2 开头的子数组 [2] [2, 3]。
固定起始下标的子数组遍历方法常用于暴力枚举解法。

// 固定起始下标
public void fixedStartIndex(List<Integer> list) {
    for (int i = 0; i < list.size(); i++) {
        for (int j = i; j < list.size(); j++) {
            System.out.println(list.subList(i, j + 1));
        }
    }
}

结果

[1]
[1, 2]
[1, 2, 3]
[2]
[2, 3]
[3]

固定结束下标

固定结束下标，首先遍历以 1 结尾的子数组 [1]，再遍历以 2 结尾的子数组 [1, 2], [2]
固定结束下标的子数组遍历方法可以产生递推关系, 采用动态规划时, 经常通过此种遍历方式, 如背包问题, 最长公共子序列/子串 LCS 问题, 最大连续子序列和/积问题，等等。

还有比如 LeetCode.1014.Best Sightseeing Pair 最佳观光组合这道题是典型的根据固定结束下标遍历子数组方法推出 O(n) 解的问题。

// 固定结束下标
public void fixedEndIndex(List<Integer> list) {
    for (int j = 0; j < list.size(); j++) {
        for (int i = 0; i <= j; i++) {
            System.out.println(list.subList(i, j + 1));
        }
    }
}

结果

[1]
[1, 2]
[2]
[1, 2, 3]
[2, 3]
[3]

固定子数组长度

固定子数组长度，先遍历出长度为 1 的子数组 [1] [2] [3]，再遍历出长度为 2 的 [1,2] [2,3]
固定子数组长度遍历方法也常用于暴力枚举，比如 LeetCode.005.LongestPalindromicSubstring 最长回文子串

// 固定子数组长度
public void fixedLength(List<Integer> list) {
    for (int length = 1; length <= list.size(); length++) {
        for (int i = 0; i + length <= list.size(); i++) {
            System.out.println(list.subList(i, i + length));
        }
    }
}

结果

[1]
[2]
[3]
[1, 2]
[2, 3]
[1, 2, 3]

前缀和/差分/哈希

前缀和 | 标签 - 小马的笔记

前缀和的思想是一种预处理，是一种以空间换时间的做法。就是先提前求得 presum[i] = nums[0] + ... + nums[i]，保存下来，以后计算的时候直接用。
假如已知 presum[] 则子数组 nums[i...j] 的和 sum(i,j) = presum[j] - presum[i-1]，也就是子数组的和可直接通过前缀和数组的差分求得。

LeetCode.560.Subarray Sum Equals K 和为K的子数组
 LeetCode.974.Subarray Sums Divisible by K 和可被K整除的子数组
 LeetCode.1248.Count Number of Nice Subarrays 统计优美子数组
523 连续的子数组和
https://leetcode-cn.com/problems/continuous-subarray-sum/

二维数组

二维数组 | 标签 - 小马的笔记

用差值数组简化四方向/八方向遍历

二维数组中，如果要找某个点的上下左右4个方向，或者周围8个方向的点的坐标，方便的做法是先定义两个 delta[] 数组定义好和当前x,y坐标的差值，然后遍历这个数组即可，不需要额外写4遍或8遍重复代码

// 四方向
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};

// 八方向
int[] dx = {-1, -1, 0, 1, 1, 1, 0, -1};
int[] dy = {0, 1, 1, 1, 0, -1, -1, -1};

int nrows = 2DArray.length, ncolumns = 2DArray[0].length;
for (int k = 0; k < 8; k++) {
    int ii = i + dx[k], jj = j + dy[k];
    if (ii >= 0 && ii < nrows && jj >= 0 && jj < ncolumns) {
      // do something
    }
}

链表

链表 | 标签 - 小马的笔记

巧用DumbHead

用一个不存储数据的 dumbHead 头结点作为新链表的头结点，可以简化操作，避免第一个结点特例的判断，最后返回 dumbHead.next 即可。

LeetCode.206.Reverse Linked List 反转链表
 LeetCode.092.Reverse Linked List II 反转链表的第m到n个结点
 LeetCode.025.Reverse Nodes in k-Group K 个一组翻转链表
 LeetCode.021.Merge Two Sorted Lists 合并两个有序链表

Floyd判圈算法/龟兔赛跑算法

**Floyd判圈算法(Floyd Cycle Detection Algorithm)**，又称 **龟兔赛跑算法(Tortoise and Hare Algorithm)**，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。

找链表中的环

有环单链表的环长、环起点和链表长
 LeetCode.141.Linked List Cycle 判断链表是否有环
 LeetCode.142.Linked List Cycle II 有环链表的环起点

判圈算法的其他应用

把 n 和 next(n) 看成链表的前后两个节点，如果有循环则此链表一定有环，使用Floyd判圈算法（快慢指针）进行有环判断
LeetCode.202.Happy Number 快乐数

Brent判圈算法

Brent’s Cycle Detection(The Teleporting Turtle)
起始令乌龟兔子指向起始节点，让乌龟保持不动，兔子走 2^i 步，即迭代一次，兔子走2步，迭代2次，兔子走4步等等。在兔子走每一步后，判断龟兔是否相遇，如果没有相遇，则让乌龟的位置变成兔子所在的位置，否则如果乌龟不动，则乌龟永远无法进入环内，随后进入新的迭代。循环下去，直至相遇或到表尾。

用 2 个指针 rabbit 和 turtle 从链表头出发。
rabbit先一步一步走，最多走2步，如果走到尽头，则无环，如果和turtle相遇，则有环，否则，本轮结束。
这个时候，把turtle放到rabbit当前位置，rabbit继续一步一步走，但是最多走4步，如果走到尽头，则无环，如果和turtle相遇，则有环，否则，本轮结束。
然后，把turtle放到rabbit当前位置，rabbit继续一步一步走，但是最多走8步，如果走到尽头，则无环，如果和turtle相遇，则有环，否则，本轮结束。

时间复杂度 O(n), 线性复杂度，并且比 Flyod 表现更好，且 Flyod 是该算法的最差表现

把链表连成环

LeetCode.061.Rotate List 旋转链表

跳跃表(skiplist)

有时候会被问到链表如果做到二分搜索，可能会有部分的人会去把链表中的值保存到数组来进行二分，但是如果知道跳跃表的话，那么这个数据结构就可以解决这个困惑，它允许快速查询一个有序连续元素的数据链表，它的效率可以做到和二分相同，都是 O(logn) 的平均时间复杂度，其空间复杂度为 O(n)。

跳跃列表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃列表的算法有同平衡树一样的渐进的预期时间边界，并且更简单、更快速和使用更少的空间。
像是redis中有序集合就使用到了跳跃表。

跳跃表的性质；
1、由很多层结构组成；
2、每一层都是一个有序的链表，排列顺序为由高层到底层，都至少包含两个链表节点，分别是前面的head节点和后面的nil节点；
3、最底层的链表包含了所有的元素；
4、如果一个元素出现在某一层的链表中，那么在该层之下的链表也全都会出现（上一层的元素是当前层的元素的子集）；
5、链表中的每个节点都包含两个指针，一个指向同一层的下一个链表节点，另一个指向下一层的同一个链表节点；

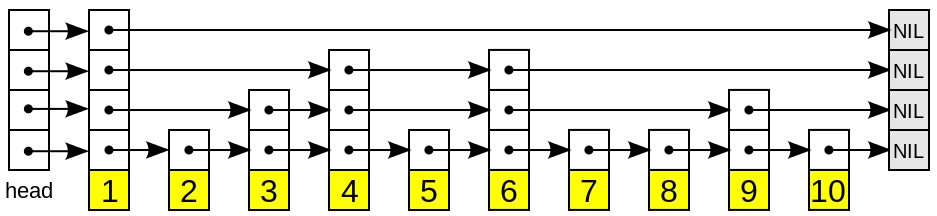
跳跃表

可以看到，这里一共有4层，最上面就是最高层（Level 3），最下面的层就是最底层（Level 0），然后每一列中的链表节点中的值都是相同的，用指针来连接着。跳跃表的层数跟结构中最高节点的高度相同。理想情况下，跳跃表结构中第一层中存在所有的节点，第二层只有一半的节点，而且是均匀间隔，第三层则存在1/4的节点，并且是均匀间隔的，以此类推，这样理想的层数就是logN。

搜索
其基本原理就是从最高层的链表节点开始，如果比当前节点要大和比当前层的下一个节点要小，那么则往下找，也就是和当前层的下一层的节点的下一个节点进行比较，以此类推，一直找到最底层的最后一个节点，如果找到则返回，反之则返回空。
跳跃表查找操作的时间复杂度是O（logN）

插入
既然要插入，首先需要确定插入的层数，这里有不一样的方法。1. 看到一些博客写的是抛硬币，只要是正面就累加，直到遇见反面才停止，最后记录正面的次数并将其作为要添加新元素的层；2. 还有就是一些博客里面写的统计概率，先给定一个概率p，产生一个0到1之间的随机数，如果这个随机数小于p，则将高度加1，直到产生的随机数大于概率p才停止，根据给出的结论，当概率为1/2或者是1/4的时候，整体的性能会比较好（其实当p为1/2的时候，也就是抛硬币的方法）。
当确定好要插入的层数以后，则需要将元素都插入到从最底层到第k层。
跳跃表插入操作的时间复杂度是O（logN）

删除
在各个层中找到包含指定值的节点，然后将节点从链表中删除即可，如果删除以后只剩下头尾两个节点，则删除这一层。
总体上，跳跃表删除操作的时间复杂度是O（logN）

跳跃表原理和实现
https://www.cnblogs.com/George1994/p/7635731.html

漫画算法：什么是跳跃表？
http://blog.jobbole.com/111731/

栈和队列

最小(大)栈

设计一个支持 push，pop，top 操作，并含有常数时间内检索最小元素方法 getMin 的栈，即最小栈。
思路分析：
在栈中实现一个方法，每一调用该方法可以获得当前栈中的最小值。
使用辅助栈，空间换时间。
把两个栈封装在一个栈中，其中的一个栈存放正常的元素，另一个栈 minStack 只存当前最小值。
push：数据栈正常操作。比较当前元素和最小栈 minStack 的栈顶，比栈顶还小则进栈，否则 push 原栈顶。
pop：数据栈正常操作。最小栈 minStack 也 pop
getMin：直接返回最小栈栈顶

LeetCode.155.Min Stack 最小栈

实现一个最大栈、最小栈
http://blog.csdn.net/u013078669/article/details/51029935

最小(大)队列

LeetCode.剑指offer.059.最大队列

单调栈

单调栈 | 标签 - 小马的笔记

单调栈(Monotone Stack)，顾名思义，是栈内元素保持一定单调性（单调递增或单调递减）的栈。这里的单调递增或递减是指的从栈顶到栈底单调递增或递减。既然是栈，就满足后进先出的特点。与之相对应的是单调队列。

单调栈的push

将一个元素插入单调栈时，为了维护栈的单调性，需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。
例如，单调递减栈中元素自底向上为 50 30 10 5 3 1，插入元素 20 时为了保证单调性需要依次弹出元素 1 3 5 10 ，操作后栈变为 50 30 20 。

单调栈应用

单调栈这种数据结构，通常应用在一维数组上。如果遇到的问题涉及前后元素之间的大小关系的话，我们可以试图用单调栈来解决。

1、单调递增栈(栈顶最大)可以找到左起第一个比当前数字小的元素。
比如数组 [2 1 4 6 5]，刚开始2入栈，数字1入栈的时候，发现栈顶元素2比较大，将2移出栈，此时1入栈。那么2和1都没左起比自身小的数字。然后数字4入栈的时候，栈顶元素1小于4，于是1就是4左起第一个小的数字。此时栈里有1和4，然后数字6入栈的时候，栈顶元素4小于6，于是4就是6左起第一个小的数字。此时栈里有1，4，6，然后数字5入栈的时候，栈顶元素6大于5，将6移除，此时新的栈顶元素4小于5，那么4就是5左起的第一个小的数字，最终栈内数字为 1，4，5。

2、单调递减栈(栈顶最小)可以找到左起第一个比当前数字大的元素。
比如数组 [2 1 4 6 5], 开始 2 入栈，1入栈看到的栈顶2就是左边第一个比1大的元素。4入栈时弹出1和2，4左边没有比他大的。6入栈时弹出4，6左边没有比他大的。5入栈时看到的栈顶6是左边第一个比他大的。

3、给定一组数，针对每个数，寻找它和它右边第一个比它大的数之间有多少个数
题目1
POJ 3250 Bad Hair Day
http://poj.org/problem?id=3250
有一群牛站成一排，每头牛都是面朝右的，每头牛可以看到他右边身高比他小的牛。给出每头牛的身高，要求每头牛能看到的牛的总数。
题目2
本题还有一个类似的题，那就是给出N块竖直的木板的高度，现在在第 i 块木板的右方加水，问可以水可以淹没多少木板。
题目3
给一个数组，返回一个大小相同的数组。返回的数组的第i个位置的值应当是，对于原数组中的第i个元素，至少往右走多少步，才能遇到一个比自己大的元素（如果之后没有比自己大的元素，或者已经是最后一个元素，则在返回数组的对应位置放上-1）
题目4
LeetCode.739.Daily Temperatures 每日温度

上面 4 个题目描述不同，其实都是相同的题，都是求每个数和它右边第一个比它大的数之间的数的个数
这是一个经典的单调栈题目，并且是纯粹的单调栈应用，没有其他复杂逻辑，非常适合作为单调栈的入门题目。

解法1、朴素的做法是双重循环遍历，时间复杂度为O(n^2)
解法2、单调栈，时间复杂度O(n)
维护一个栈顶元素最小的单调栈，从前往后遍历数组，当栈为空或当前元素小于栈顶时入站，当前元素大于等于栈顶时，由于会破坏单调栈需要从栈顶依次弹出小于等于当前元素的数，并依次计算和当前元素的间隔(下标差)，直到遇到大于当前元素的栈顶元素。

POJ 3250 Bad Hair Day 单调栈代码详解
https://blog.csdn.net/zuzhiang/article/details/78134848

LeetCode Monotone Stack Summary 单调栈小结
https://www.cnblogs.com/grandyang/p/8887985.html

如何选择递增还是递减？

是选择 单调递增栈 还是 单调递减栈 取决于问题的触发计算时机，以下面两个经典的单调栈问题为例
LeetCode.042.Trapping Rain Water 接雨水
 LeetCode.084.Largest Rectangle in Histogram 柱状图中最大的矩形

接雨水问题中，每次形成一个凹槽后才能计算雨水量，也就是遇到递减到递增的转折点时触发计算，所以维护一个单调递减栈，当前元素比栈顶小时直接入栈不计算，遇到比栈顶大的元素时（这时就是到了递减到递增的转折点）出栈开始计算。

矩形最大面积问题中，我们需要找到每个高度左右第一个比他小的位置下标作为左右边界，所以这个问题需要在遇到递增到递减的转折点时触发计算，所以维护一个单调递增栈，当前元素比栈顶大时入栈，比栈顶小时就遇到了右侧比栈顶小的边界，也就是递增到递减的转折点，此时栈顶的下一个元素就是左侧边界。

最后补最大/小值触发计算

单调栈应用中会遇到一个问题，就是假如使用单调递增栈且原数组中元素本身就是完全单调递增的，就没有触发计算的时机，这时可以使用一个单调栈问题中经常用到的技巧，我们在原数组最后补一个虚拟的不可能在数组中存在的最小/大值，最后将其压入栈中，以便触发计算。

单调栈参考资料：
https://www.cnblogs.com/grandyang/p/8887985.html；
https://blog.csdn.net/liujian20150808/article/details/50752861

单调队列

单调队列(Monotone Queue)，顾名思义就是单调递增或者单调递减的队列。
单调队列不是真正的队列。因为队列都是FIFO的，统一从队尾入列，从对首出列。但单调队列是从队尾入列，从队首或队尾都可以出列，不遵守FIFO规则，其实是一个双端队列，也就是通常说的Deque。

单调队列的操作
对于单调(递增)队列，每次添加新元素时跟队尾比较，如果队尾元素值大于待入队元素，则将对尾元素从队列中弹出，重复此操作，直到队列为空或者队尾元素小于待入队元素。然后，再把待入队元素添加到队列末尾。
比如当前单调递增队列中有元素 1 4 7 10 , 队尾是10，元素 5 入队时需要依次从队尾弹出 10 和 7 ，然后再把 5 入队尾，队列变为 1 4 5

单调最烈的应用
单调(递增)队列可以用来求滑动窗口的最小值。同理，单调(递减)队列可以用来求滑动窗口的最大值。其算法复杂度都是O(n)。

滑动窗口中的最大/小值

本题大意是给出一个长度为 n 的数组，编程输出每 k 个连续的数中的最大值和最小值。
给定一个整数数组nums，给定一个整数k，k为窗口大小，滑动窗口，每次向右滑动一格，求每一个窗口中的元素的最大值。

239 Sliding Window Maximum
https://leetcode-cn.com/problems/sliding-window-maximum/

此问题是 RMQ 问题的简化特例
RMQ 是英文 Range Maximum/Minimum Query 的缩写，表示区间最大（最小）值。

以求滑动窗口中的最大值为例
1、暴力求解，每次从一个窗口的起点开始向后遍历k个数字，然后求出最大值，时间复杂度 O(n^2)
2、维护一个长度为 k 的单调递减队列（队尾最小），依次把元素加入队列，如果比队尾小直接入队，如果比队尾大则弹出队尾直到比队尾小，每次队列的队头元素就是这个滑动窗口中的最大值。注意，当滑动窗口长度超过 k 时，队头元素要出队。

用两个栈实现一个队列

真正性能高的实现方法：
两个栈 s1 和 s2，s1 只用于入队，s2 只用于出队。
入队时，将元素压入 s1
出队时，判断 s2 是否为空，如不为空，则直接弹出顶元素；如为空，则将 s1 的元素逐个”倒入” s2，把最后一个元素弹出并出队。
这个思路，避免了反复“倒”栈，仅在需要时才“倒”一次。
此方法 EnQueue 时间复杂度 O(1)，DeQueue 也可以达到 O(1) 的摊还复杂度，非常好。

LeetCode.剑指offer.009.用两个栈实现队列
 LeetCode.232.Implement Queue using Stacks 用栈实现队列

用两个栈实现一个队列——我作为面试官的小结
https://www.cnblogs.com/wanghui9072229/archive/2011/11/22/2259391.html

用一个或两个队列实现栈

LeetCode.225.Implement Stack using Queues 用队列实现栈

用一个队列或两个队列都可以模拟栈，但是要两个栈才能模拟一个队列

类设计

类设计 | 标签 - 小马的笔记

实现生产者消费者模式

Java阻塞队列实现生产者消费者

public class ProducerConsumerBlockingQueue {
    private BlockingQueue<String> blockingQueue;

    private class Producer extends Thread {
        @Override
        public void run() {
            while (true) {
                try {
                    produce();
                    Thread.sleep((long)(Math.random() * 1000));
                } catch (Exception e) {
                    e.printStackTrace();
                }
            }
        }

        void produce() throws  Exception {
            String element = "元素" + (int)(Math.random() * 100);
            blockingQueue.put(element);
            System.out.println("生产者放入 " + element + " [" + blockingQueue.size() + "]");
        }
    }

    private class Consumer extends Thread {
        @Override
        public void run() {
            while (true) {
                try {
                    consume();
                    Thread.sleep((long)(Math.random() * 1000));
                } catch (Exception e) {
                    e.printStackTrace();
                }
            }
        }

        void consume() throws Exception {
            System.out.println("消费者取出 " + blockingQueue.take() + " [" + blockingQueue.size() + "]");
        }
    }

    @Test
    public void test() throws Exception {
        blockingQueue = new LinkedBlockingDeque<>(10);
        Producer producer = new Producer();
        Consumer consumer = new Consumer();
        producer.start();
        consumer.start();
        // 主线程等待生产者和消费组执行结束
        producer.join();
        consumer.join();
    }
}

实现LRU缓存

LeetCode.146.LRU Cache 实现LRU缓存

实现LFU缓存

LeetCode.460.LFU Cache 实现LFU缓存

实现推特

LeetCode.355.Design Twitter 设计推特

实现Trie树/前缀树/字典树

LeetCode.208.Implement Trie (Prefix Tree) 实现 Trie (前缀树/字典树)

Trie树/前缀树/字典树

Trie 树，又叫字典树、前缀树（Prefix Tree）、单词查找树或键树，是一种多叉树结构。

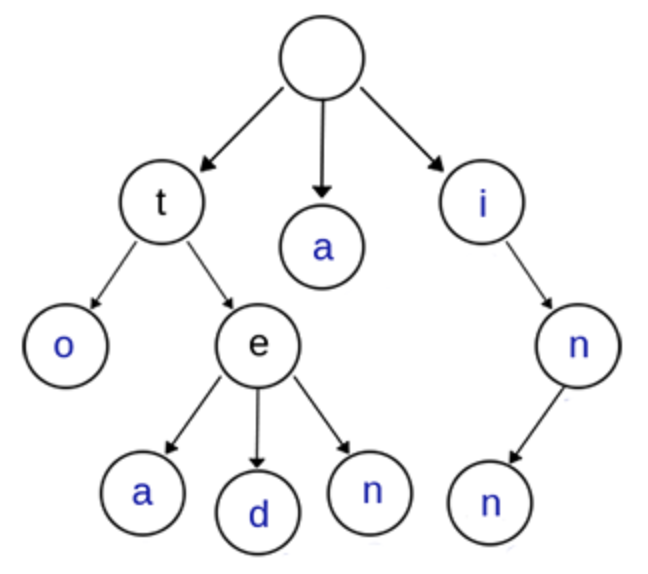
Trie树

上图是一棵 Trie 树，表示了关键字集合 {“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”}

通常在实现的时候，会在节点结构中设置一个标志，用来标记该结点处是否构成一个单词（关键字）。

优点

插入和查询的效率很高，都为 O(m)，其中 m 是待插入/查询的字符串的长度。
关于查询，会有人说 hash 表时间复杂度是 O(1) 不是更快？但是，哈希搜索的效率通常取决于 hash 函数的好坏，若一个坏的 hash 函数导致很多的冲突，效率并不一定比 Trie 树高。
Trie 树中不同的关键字不会产生冲突。
Trie 树只有在允许一个关键字关联多个值的情况下才有类似 hash 碰撞发生。
Trie 树不用求 hash 值，对短字符串有更快的速度。通常，求 hash 值也是需要遍历字符串的。
Trie 树可以对关键字按字典序排序。

缺点

当 hash 函数很好时，Trie 树的查找效率会低于哈希搜索。
空间消耗比较大。

前缀树和哈希表对比

尽管哈希表可以在 O(1) 时间内寻找键值，却无法高效的完成以下操作：
找到具有同一前缀的全部键值。
按词典序枚举字符串的数据集。
此外，随着哈希表大小增加，会出现大量的冲突。

Trie树应用

字符串检索

检索/查询功能是 Trie 树最原始的功能。思路就是从根节点开始一个一个字符进行比较：
如果沿路比较，发现不同的字符，则表示该字符串在集合中不存在。
如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表一个关键字）。

class TrieNode {
    boolean isKey;   // 标记该节点是否代表一个关键字
    TrieNode[] children[26]; // 各个子节点
}

词频统计

修改节点结构，用一个整型变量 count 来计数。
对每一个关键字执行插入操作，若已存在，计数加1，若不存在，插入后count置1。

class TrieNode {
    int count;   // 记录该节点代表的单词的个数
    TrieNode[] children[26]; // 各个子节点
}

可能有人要说了，词频统计简单啊，一个hash或者一个堆就可以打完收工，但问题来了，如果内存有限呢？还能这么玩吗？所以这里我们就可以用trie树来压缩下空间，因为公共前缀都是用一个节点保存的。

前缀匹配

从根节点开始对 prefix 的每个字符进行比较，如果发现 prefix 的某个字符不在前缀树中，则 prefix 在前缀树中不存在。时间复杂度为 O(n)，n 是目标前缀 prefix 的长度。
trie 树前缀匹配常用于搜索提示和自动补全。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

字典序排序

Trie树可以对大量字符串按字典序进行排序，思路也很简单：遍历一次所有关键字，将它们全部插入trie树，树的每个结点的所有儿子很显然地按照字母表排序，然后先序遍历输出Trie树中所有关键字即可。

前缀树的实现

一般使用邻接表结构存储前缀树，以只包含小写字母的前缀树为例
前缀树结点定义如下：

// 前缀树结点
private static class TrieNode {
    private TrieNode[] children; // 子树结点数组，下标为 i 的子树表示以字符 i+'a' 为根的子树
    private int count; // 子树个数
    private boolean isEnd; // 当前节点是否单词结尾

    private TrieNode() {
        children = new TrieNode[26];
        count = 0;
        isEnd = false;
    }
}

所以真正的实现如下图所示：

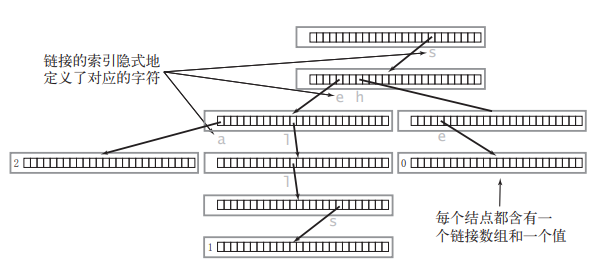
Trie的存储结构

完整代码实现见
LeetCode.208.Implement Trie (Prefix Tree) 实现 Trie (前缀树/字典树)

insert(key) 插入key

从根开始依次搜索 key 的每个字符，对于字符 ch
1、如果对应子树 children[ch - 'a'] 存在，在子树上继续搜索 key 的下一个字符。
2、如果对应子树 children[ch - 'a'] 不存在，创建一个新的节点，存储到父节点的 children[ch - 'a'] 位置，同样在子树上继续搜索 key 的下一个字符。
重复以上步骤，直到到达 key 的最后一个字符，然后将当前节点标记为结束节点，完成。
时间复杂度 O(m)，m 是 key 的长度

// 插入单词 word
public void insert(String word) {
    TrieNode trieNode = root;
    for (int i = 0; i < word.length(); i++) {
        char c = word.charAt(i);
        if (trieNode.containChar(c)) {
            trieNode = trieNode.get(c);
        } else {
            trieNode = trieNode.insertChar(c);
        }
    }
    trieNode.isEnd = true;
}

search(key) 查找key

从根开始依次搜索 key 的每个字符，对于字符 ch
1、如果对应子树 children[ch - 'a'] 存在，在子树上继续搜索 key 的下一个字符。
2、如果对应子树 children[ch - 'a'] 不存在，返回 false
如果 key 的所有字符在前缀树中都存在，且最后一个字符对应的结点 isEnd 标识为 true，则返回true。
时间复杂度 O(m)，m 是 key 的长度

// 判断单词 word 是否在前缀树中，单词 word 在前缀树中时返回 true
public boolean search(String word) {
    TrieNode trieNode = root;
    for (int i = 0; i < word.length(); i++) {
        char c = word.charAt(i);
        if (!trieNode.containChar(c)) {
            return false;
        } else {
            trieNode = trieNode.get(c);
        }
    }
    return trieNode.isEnd;
}

startsWith(prefix) 判断前缀是否存在

和 search 相似，只不过最后不需要判断 isEnd 是否为true
时间复杂度 O(m)，m 是 key 的长度

// 判断前缀 prefix 是否在前缀树中
public boolean startsWith(String prefix) {
    TrieNode trieNode = root;
    for (int i = 0; i < prefix.length(); i++) {
        char c = prefix.charAt(i);
        if (!trieNode.containChar(c)) {
            return false;
        } else {
            trieNode = trieNode.get(c);
        }
    }
    return true;
}

并查集(UnionFind)

并查集主要用于解决元素分组的问题。它管理一系列不相交的集合，并支持两种操作：
合并（Union）：把两个不相交的集合合并为一个集合。
查询（Find）：查询两个元素是否在同一个集合中。

并查集中有多个不相交的子集，每个子集有一个元素作为代表，称为集合的代表元或根。
每个子集内的所有元素组织成以代表元为根的树形结构。
这里的子集，也可以叫子树，或者叫不同的联通分量。

并查集的存储结构

使用数组 int[] parent 作为并查集的存储结构。
用 index -> value 表达指向关系，对于每一个元素 x， parent[x] 指向 x 在树形结构上的父亲节点。如果 x 是根节点，则令 parent[x] = x

find(x) 查找操作

find(x) 查找元素 x 所属子集的根节点。
可以沿着 parent(x) 不断在树形结构中向上移动，直到到达根节点。
find(x) 方法可以被用来确定两个元素是否属于同一子集。判断两个元素是否属于同一集合，只需要看他们的代表元是否相同即可。

迭代实现：

// 在并查集中查找 x 的根 - 迭代
public int findIterative(int x) {
    while (parent[x] != x) {
        x = parent[x];
    }
    return x;
}

递归实现：

// 在并查集中查找 x 的根 - 递归
public int find(int x) {
    return parent[x] == x ? x : find(parent[x]);
}

路径压缩

比如我们对 0 - 10 内的整数进行分组，奇数一组，偶数一组，每组的根是最小元素，得到下面这两个子树

9 -> 7 -> 5 -> 3 -> 1
10 -> 8 -> 6 -> 4 -> 2 -> 0

假如查 9 的根需要依次向上遍历到 1 才行，路径很长，其实我们需要的只是找 9 的根，中间这些关联关系都是没用的，所以可以将路径压缩为 9 -> 1，这就是路径压缩。

路径压缩可以在查找过程中动态的进行，直接修改 find(x) 方法， 在查询的过程中把沿途的每个节点的父节点都设为根节点即可。

// 在并查集中查找 x 的根 - 递归并带有路径压缩
public int find(int x) {
    return parent[x] == x ? x : (parent[x] = find(parent[x]));
}

路径压缩后刚才例子中的并查集就变为：

2 -> 0
3 -> 1
4 -> 0
5 -> 1
6 -> 0
7 -> 1
8 -> 0
9 -> 1
10 -> 0

union(x,y) 合并操作

union(x, y) 将两个元素 x 和 y 所属的子集合并成同一个集合。
常用的合并方法是：令 x 所在子树的根指向 y 所在子树的根。

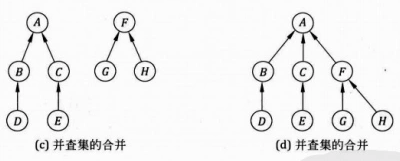
并查集的合并

按秩合并

未优化的合并方法的问题是，在任何情况下都是将 x 子树的根指向 y 子树，但其实某些情况下反过来操作会使合并后的树深度更低。
比如，如果将一个深度是 3 的子树的根指向一个深度是 1 的子树的根，则合并后的子树深度是 4，但如果反过来，合并后的子树深度还是 3

所以，我们应该把简单的树往复杂的树上合并，而不是相反。这就是对合并方法的优化，叫按秩合并：
我们用一个数组 ranks[] 记录每个根节点对应的树的深度（这里叫秩），如果不是根节点，其 rank 值相当于以它作为根节点的子树的深度。一开始，把所有元素的 rank 值设为 1。合并时比较两个根节点，把 rank 较小者往较大者上合并。也就是，如果 ranks[x] < ranks[y] 则让 x 所在子树的根指向 y 所在子树的根，即 parent[find(x)] = find(y)，从而保证合并后深度不超过 ranks[y]

按秩合并和路径压缩两种优化一起使用，压缩后需要谨慎维护 ranks 数组，否则会出现 ranks 数据不准确。

统计联通分量个数

统计 parent[i] == i 的元素个数即可。

带权并查集

399 除法求值
https://leetcode-cn.com/problems/evaluate-division/

并查集的实现

并查集实现，有路径压缩，但没实现按秩合并

public class UnionFind {
    int length = 0;
    int[] parent;

    // 初始化一个长度为 length 的并查集
    public UnionFind(int length) {
        this.length = length;
        this.parent = new int[length];
        // 初始时，每个元素都是自己的根
        for (int i = 0; i < length; i++) {
            parent[i] = i;
        }
    }

    // 合并 x 和 y，即将 x 的根节点指向 y
    public void union(int x, int y) {
        int xParent = find(x);
        int yParent = find(y);
        if (xParent != yParent) {
            parent[xParent] = y;
        }
    }

    // 在并查集中查找 x 的根 - 递归并带有路径压缩
    public int find(int x) {
        return parent[x] == x ? x : (parent[x] = find(parent[x]));
    }

    // 在并查集中查找 x 的根 - 迭代
    public int findIterative(int x) {
        while (parent[x] != x) {
            x = parent[x];
        }
        return x;
    }

    // 打印并查集
    public void print() {
        Set<Integer> valueSet = new HashSet<>();
        for (int i = 0; i < length; i++) {
            if (parent[i] != i) {
                valueSet.add(parent[i]);
            }
        }
        for (int i = 0; i < length; i++) {
            // 只遍历有父节点的叶子节点，即 i 指向其他结点 且 i 不被其他结点指向
            if (parent[i] != i && !valueSet.contains(i)) {
                int j = i;
                while (j != parent[j]) {
                    System.out.print(j + " -> ");
                    j = parent[j];
                }
                System.out.println(j);
            }
        }
    }
}

树和二叉树

二叉树 | 标签 - 小马的笔记

完全二叉树(Complete Binary Tree)

完全二叉树(Complete Binary Tree)
在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树。

完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树

二叉搜索树(二叉排序树)(BST)

二叉查找树(也叫二叉搜索树)（Binary Search Tree）就是二叉排序树（Binary Sort Tree）

设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点，那么会有y.key<=x.key；如果y是x右子树中的一个节点，那么有y.key>=x.key。

BST | 标签 - 小马的笔记

查找与性能分析O(logn)->O(n)

若假设树的高度是h，那么查找过程的时间复杂度就是O(h)。
若n个结点的二叉搜索树是平衡的，查找复杂度为O(logn)，最坏情况下（比如用有序数组创建BST），二叉查找树退化成了一棵具有n个结点的线性链（单边树），查找复杂度为O(n)。

递归实现：

//递归实现
Tree_Search(x, k):
if x == NIL or x.key == k :
    return x
if k < x.key
    return Tree_Search(x.left, k)
else return Tree_Search(x.right, k)

非递归迭代实现：

//非递归迭代实现
Tree_Search(x, k) :
while x!=NIL and k!=x.key:
    if k < x.key
        x = x.left
    else x = x.right
return x

深入理解二叉搜索树（BST）
https://blog.csdn.net/u013405574/article/details/51058133

把BST转换为双向链表

http://blog.csdn.net/brucehb/article/details/58381745

平衡二叉树(AVL)

AVL树是根据它的发明者G. M. Adelson-Velskii和E. M. Landis命名的。AVL树本质上还是一棵二叉搜索树，它的特点是：
本身首先是一棵二叉查找树。带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

平衡二叉树定义(AVL)：它或者是一颗空树，或者具有以下性质的二叉树：它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。

平衡因子(bf)：结点的左子树的深度减去右子树的深度，那么显然-1<=bf<=1

平衡二叉树是在二叉排序树(BST)上引入的，就是为了解决二叉排序树的不平衡性导致时间复杂度大大下降，那么AVL就保持住了(BST)的最好时间复杂度O(logn)，所以每次的插入和删除都要确保二叉树的平衡（通过旋转实现）。

平衡二叉树很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

平衡二叉树详解
https://blog.csdn.net/u010442302/article/details/52713585

红黑树(RBT)

R-B Tree，全称是Red-Black Tree，又称为“红黑树”，它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

红黑树是一种近似平衡的二叉查找树，它能够确保任何一个节点的左右子树的高度差不会超过二者中较低那个的一陪。

红黑树的特性:
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

红黑树的插入

将一个节点插入到红黑树中，需要执行哪些步骤呢？首先，将红黑树当作一颗二叉查找树，将节点插入；然后，将节点着色为红色；最后，通过旋转和重新着色等方法来修正该树，使之重新成为一颗红黑树。

1、把红黑树当做BST插入结点

第一步: 将红黑树当作一颗二叉查找树，将节点插入。
红黑树本身就是一颗二叉查找树，将节点插入后，该树仍然是一颗二叉查找树。也就意味着，树的键值仍然是有序的。此外，无论是左旋还是右旋，若旋转之前这棵树是二叉查找树，旋转之后它一定还是二叉查找树。这也就意味着，任何的旋转和重新着色操作，都不会改变它仍然是一颗二叉查找树的事实。
好吧？那接下来，我们就来想方设法的旋转以及重新着色，使这颗树重新成为红黑树！

2、把插入结点染为红色

第二步：将插入的节点着色为”红色”。
为什么着色成红色，而不是黑色呢？为什么呢？在回答之前，我们需要重新温习一下红黑树的特性：
(1) 每个节点或者是黑色，或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]
(4) 如果一个节点是红色的，则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
将插入的节点着色为红色，不会违背”特性(5)”！少违背一条特性，就意味着我们需要处理的情况越少。接下来，就要努力的让这棵树满足其它性质即可；满足了的话，它就又是一颗红黑树了。

为什么将插入结点看做红色？

因为要满足红黑树的这五条性质，如果我们插入的是黑色节点，那就违反了性质五，需要进行大规模调整，如果我们插入的是红色节点，那就只有在要插入节点的父节点也是红色的时候违反性质四或者是当插入的节点是根节点时，违反性质二，所以，我们把要插入的节点的颜色变成红色。

3、旋转与着色使之再次成为红黑树

在树的结构发生改变时（插入或者删除操作），红黑树的条件可能被破坏，需要通过调整使得查找树重新满足红黑树的条件。调整可以分为两类：一类是颜色调整，即改变某个节点的颜色；另一类是结构调整，集改变检索树的结构关系。结构调整过程包含两个基本操作：左旋（Rotate Left），右旋（RotateRight）。

红黑树的应用

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。
例如，Java集合中的TreeSet和TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

1、广泛用于C++的STL中,map和set都是用红黑树实现的.
2、著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一颗红黑树上,每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间.
3、IO多路复用epoll的实现采用红黑树组织管理sockfd，以支持快速的增删改查.
4、ngnix中,用红黑树管理timer,因为红黑树是有序的,可以很快的得到距离当前最小的定时器.
5、java中TreeMap的实现.

红黑树与AVL对比

平衡二叉树是一种严格的平衡树，平衡因子小于等于1。由于维护这种高度平衡所付出的代价比从中获得的效率收益还大，故而实际的应用不多，更多的地方是用追求局部而不是非常严格整体平衡的红黑树.当然,如果应用场景中对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树.

AVL 和RBT 都是二叉查找树的优化。其性能要远远好于二叉查找树。他们之间都有自己的优势，其应用上也有不同。
结构对比： AVL的结构高度平衡，RBT的结构基本平衡。平衡度AVL > RBT.
查找对比： AVL 查找时间复杂度最好，最坏情况都是O(logN)。RBT 查找时间复杂度最好为O(logN)，最坏情况下比AVL略差。
插入删除对比：

AVL的插入和删除结点很容易造成树结构的不平衡，而RBT的平衡度要求较低。因此在大量数据插入的情况下，RBT需要通过旋转变色操作来重新达到平衡的频度要小于AVL。
如果需要平衡处理时，RBT比AVL多一种变色操作，而且变色的时间复杂度在O(logN)数量级上。但是由于操作简单，所以在实践中这种变色仍然是非常快速的。
当插入一个结点都引起了树的不平衡，AVL和RBT都最多需要2次旋转操作。但删除一个结点引起不平衡后，AVL最多需要logN 次旋转操作，而RBT最多只需要3次。因此两者插入一个结点的代价差不多，但删除一个结点的代价RBT要低一些。
AVL和RBT的插入删除代价主要还是消耗在查找待操作的结点上。因此时间复杂度基本上都是与O(logN) 成正比的。
总体评价：大量数据实践证明，RBT的总体统计性能要好于平衡二叉树。

二叉查找树、平衡二叉树、红黑树、B-/B+树性能对比
https://blog.csdn.net/z702143700/article/details/49079107

浅谈AVL树,红黑树,B树,B+树原理及应用
https://blog.csdn.net/whoamiyang/article/details/51926985

红黑树(一)之原理和算法详细介绍
http://www.cnblogs.com/skywang12345/p/3245399.html

最容易懂得红黑树
https://blog.csdn.net/sun_tttt/article/details/65445754

史上最清晰的红黑树讲解（上）（结合Java TreeMap讲解）
https://www.cnblogs.com/CarpenterLee/p/5503882.html

漫画：什么是红黑树？ - 程序员小灰
http://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw==&mid=2653191832&idx=1&sn=12017161025495c6914b5ab9397baa59

B-树(B树)

B-树就是B树，也就是英文中的B-Tree，中间是横线不是减号，一般直接读作B树（读作B减树不规范，但好多人这么读）
B树和 B+ 树中的B不是 Binary 二叉的意思，而是 Balanced 平衡。

一个m阶的B树具有如下几个特征：
1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
3.每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

为什么数据库索引使用B树？

数据库索引是存储在磁盘上的，索引大小可能有几个G甚至更多。当利用索引查询的时候，不能把整个索引都加载到内存中，只能逐一加载每个磁盘页，这里的磁盘页对应着索引树的结点。每次加载一个结点，都需要进行一次磁盘IO，磁盘IO的次数等于索引树的高度。

为了减少磁盘IO的次数，需要把原本“瘦高”的树结构变得“矮胖”。B树是一种多路平衡查找树，由于是多叉的，对于同样的结点个数n，B树比平衡二叉树的高度更小，这就是B树相对于平衡二叉树的优点。

由于B树每个节点上有多个key值，所以查询时比较次数其实不比平衡二叉树少，但相对于耗时的磁盘IO，内存中的比较耗时几乎可以忽略。只要高度足够低，IO次数足够少，就可以提高查找性能。

漫画：什么是B-树？
http://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw==&mid=2653190965&idx=1&sn=53f78fa037386f85531832cd5322d2a0

B+树

B+树是B树的一个升级版，相对于B树来说B+树更充分的利用了节点的空间，让查询速度更加稳定，其速度完全接近于二分法查找。

一个m阶的B+树具有如下几个特征：
1.有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。
2.所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
3.所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

B+ 树分为 leaf page，也就是叶子节点，也叫数据页，存储数据， index page，非叶子结点，也叫索引页，存储索引。

B+树与B树对比

B+树相比于B树的优势：
1、IO次数更少(磁盘IO代价低)
相对于B树，B+树每个节点存储的关键字数更多，这就意味着，数据量相同的情况下，B+树的层级更少(高度更低、更矮胖)，所以IO次数更少，查询数据更快。
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说I/O读写次数也就降低了。

其实，当初设计B+树的目的就是为了磁盘适应文件系统的磁盘访问。
在数据库中，B+树的高度一般都在2~~4层，也就是说查找某一键值的行记录最多只需要2~~4次IO。

2、查询性能稳定
B+树中所有关键字指针都存在叶子节点，所以每次查询都必须最终查到叶子节点上，而B树只要找到匹配元素即停止。所以B树查找性能并不稳定（最好情况只查根节点，最坏情况查到叶子节点），而B+树每次查找都是稳定的。
由于内部结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

3、范围查询方便(顺序遍历)
B树中做范围查询只能先找到边界点（比作左边界），再做中序遍历直到右边界，很繁琐。由于B+树中所有叶子节点形成有序链表，所以B+树中做范围查询只需先找到边界点（比如左边界），然后在链表上顺序遍历到右边界即可。
B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题，而B+树只需要遍历叶子节点就可以解决对全部关键字信息的扫描，所以对于数据库中频繁使用的range query，B+树有着更高的性能。

漫画：什么是B+树？
https://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw==&mid=2653191027&idx=1&sn=4ba22e3ec8bd149f69fc0aba72e4347e

浅谈AVL树,红黑树,B树,B+树原理及应用
https://blog.csdn.net/whoamiyang/article/details/51926985

B树与B+树
https://blog.csdn.net/guoziqing506/article/details/64122287

B树和B+树与索引

B树主要应用于文件系统以及部分数据库索引，比如著名的非关系数据库MongoDB
而大部分关系型数据库，比如mysql，则使用B+树作为索引。

在 MySQL 中，主要有四种类型的索引，分别为： B-Tree 索引， Hash 索引， Fulltext 索引和 R-Tree 索引。我们主要分析B-Tree 索引。

B-Tree 索引是 MySQL 数据库中使用最为频繁的索引类型，除了 Archive 存储引擎之外的其他所有的存储引擎都支持 B-Tree 索引。Archive 引擎直到 MySQL 5.1 才支持索引，而且只支持索引单个 AUTO_INCREMENT 列。

不仅仅在 MySQL 中是如此，实际上在其他的很多数据库管理系统中B-Tree 索引也同样是作为最主要的索引类型，这主要是因为 B-Tree 索引的存储结构在数据库的数据检索中有非常优异的表现。

一般来说， MySQL 中的 B-Tree 索引的物理文件大多都是以 Balance Tree 的结构来存储的，也就是所有实际需要的数据都存放于 Tree 的 Leaf Node(叶子节点) ，而且到任何一个 Leaf Node 的最短路径的长度都是完全相同的，所以我们大家都称之为 B-Tree 索引。当然，可能各种数据库（或 MySQL 的各种存储引擎）在存放自己的 B-Tree 索引的时候会对存储结构稍作改造。如 Innodb 存储引擎的 B-Tree 索引实际使用的存储结构实际上是 B+Tree，也就是在 B-Tree 数据结构的基础上做了很小的改造，在每一个Leaf Node 上面出了存放索引键的相关信息之外，还存储了指向与该 Leaf Node 相邻的后一个 LeafNode 的指针信息（增加了顺序访问指针），这主要是为了加快检索多个相邻 Leaf Node 的效率考虑。

B-树和B+树的应用：数据搜索和数据库索引
http://blog.jobbole.com/107800/

哈夫曼树

线段树(Segment Tree)

线段树（segment tree），顾名思义，是用来存放给定区间（segment, or interval）内对应信息的一种数据结构。
线段树更新（update）的操作为 O(logn)，区间查询（range query）的操作也为 O(logn)
从数据结构的角度来说，线段树是用一个完全二叉树来存储对应于其每一个区间（segment）的数据。该二叉树的每一个结点中保存着相对应于这一个区间的信息。

给定一个长度为 N 的数组 arr，其所对应的线段树 T 各个结点的含义如下：

T 的根结点代表整个数组所在的区间对应的信息，及 arr[0:N]（不含N)所对应的信息。
T 的每一个叶结点存储对应于输入数组的每一个单个元素构成的区间 arr[i] 所对应的信息，此处 0≤i<N
T 的每一个中间结点存储对应于输入数组某一区间 arr[i:j] 对应的信息，此处 0≤i<j<N

以根结点为例，根结点代表 arr[0:N] 区间所对应的信息，接着根结点被分为两个子树，分别存储 arr[0:(N-1)/2] 及 arr[(N-1)/2+1:N] 两个子区间对应的信息。也就是说，对于每一个结点，其左右子结点分别存储母结点区间拆分为两半之后各自区间的信息。也就是说对于长度为 N 的输入数组，线段树的高度为 logN

对于一个线段树来说，其应该支持的两种操作为：

Update：更新输入数组中的某一个元素并对线段树做相应的改变。
Query：用来查询某一区间对应的信息（如最大值，最小值，区间和等）。

线段树（segment tree)，看这一篇就够了
https://blog.csdn.net/Yaokai_AssultMaster/article/details/79599809

题中的分治法用到了线段树，但不是很好理解
LeetCode.053.Maximum Subarray 最大连续子序列和

LSM Tree

Log Structured-Merge Tree 是一种分层，有序，面向磁盘的数据结构，其核心思想是充分利用磁盘顺序写速度大于随机写的特点，将随机写的操作都在内存里进行，当内存达到一定阈值后，使用顺序写一次性刷到磁盘里。
LSM 被设计来提供比传统的 B+ 树或者 ISAM 更好的写操作吞吐量。

各种强大的 NoSQL，比如Hbase，Cassandra，Leveldb，RocksDB，MongoDB，TiDB，Elasticsearch 等等，其底层使用的数据结构都是仿照 Google 的 BigTable 中使用的 LSM Tree，

像Oracle、SQL Server、DB2、MySQL (InnoDB)和 PostgreSQL 这些传统的关系数据库依赖的底层存储引擎是基于 B-Tree 开发的；
而像Cassandra、Elasticsearch (Lucene)、Google Bigtable、Apache HBase、LevelDB 和 RocksDB 这些当前比较流行的 NoSQL 数据库存储引擎是基于 LSM 树开发的。

图

Graph | 标签 - 小马的笔记

Island Perimeter
https://leetcode-cn.com/problems/island-perimeter/
被围绕的区域
https://leetcode-cn.com/problems/surrounded-regions/
Flood Fill
https://leetcode-cn.com/problems/flood-fill/
Employee Importance
https://leetcode-cn.com/problems/employee-importance/

基本概念

图是很多节点 V 和边 E 的集合，即可以表示为有序对 G=(V, E)

顶点的度：和顶点相连的边的个数。

有 n 个顶点的有向图，边的最大个数是 n(n-1), 因为以每个顶点为起点的边有最多有 n-1 条
有 n 个顶点的无向图，边的最大个数是 n(n-1)/2, 因为是无向图，边的最大个数是有向图边最大个数除以 2
边个数达到最大个数的图，叫完全图。

图的存储结构

邻接矩阵

邻接表

图的遍历

图的遍历就是从图中的某个顶点出发，按某种方法对图中的所有顶点访问且仅访问一次。
为了保证图中的顶点在遍历过程中仅访问一次，要为每一个顶点设置一个访问标志。
通常图的遍历有两种方法：深度优先搜索(DFS)和广度优先搜索(BFS)。
这两种算法对有向图与无向图均适用。

数据结构(17)–图的遍历DFS和BFS
http://blog.csdn.net/u010366748/article/details/50792759

算法导论–图的遍历（DFS与BFS）
http://blog.csdn.net/luoshixian099/article/details/51897538

深度优先搜索(DFS)

从图中某个顶点 v0 出发，首先访问 v0;
访问结点 v0 的第一个邻接点，以这个邻接点 vt 作为一个新节点，访问 vt 所有邻接点。直到以 vt 出发的所有节点都被访问到，回溯到 v0 的下一个未被访问过的邻接点，以这个邻结点为新节点，重复上述步骤。直到图中所有与 v0 相通的所有节点都被访问到。
若此时图中仍有未被访问的结点，则另选图中的一个未被访问的顶点作为起始点。重复深度优先搜索过程，直到图中的所有节点均被访问过。

遍历图的过程实质上是对每个顶点查找其邻接点的过程。其耗费的时间则取决于所采用的存储结构。
当使用二维数组表示邻接矩阵作图的存储结构时，查找每个顶点的邻接点所需时间为 O(n^2)，其中 n 为顶点数。
而当以邻接表作图的存储结构时，找邻接点所需时间为 O(e), 其中 e 为无向图中边的数目或有向图中弧的数目。由此，当以邻接表作存储结构时，深度优先搜遍遍历图的时间复杂度为 O(n+e)

DFS | 标签 - 小马的笔记

在二维数组中进行DFS/BFS

算法题中，经常会用二维数组作为图的存储结构，因为直观且简单，所以直接在二维数组上进行 DFS/BFS 是非常常见的题目。

二维数组 | 标签 - 小马的笔记

LeetCode.200.Number of Islands 岛屿个数
 LeetCode.695.Max Area of Island 岛屿的最大面积
 LeetCode.剑指offer.013.机器人的运动范围
 LeetCode.221.Maximal Square 最大正方形

假如我们需要保存二维数组的结点，比如 BFS 中需要用队列存储结点，Java 中有两种方法：使用 Pair 值对，或者一个长度为2的数组

Queue<Pair<Integer, Integer>> queue = new LinkedList<>();
Queue<int[]> queue = new LinkedList<>();

在解空间中进行DFS/回溯

LeetCode.365.Water and Jug Problem 水壶问题

LeetCode.126.Word Ladder II 单词接龙 II

在二叉树上进行DFS/BFS

二叉树的 DFS 就是先序遍历或中序遍历
二叉树的 BFS 就是层次遍历。
在树中的搜索，一般也直接把先序遍历成为 DFS

广度优先搜索(BFS)/层次遍历

广度优先搜索(BFS)
BFS 类似与树的层次遍历，从源顶点 s 出发，依照层次结构，逐层访问其他结点。即访问到距离顶点 s 为 k 的所有节点之后，才会继续访问距离为 k+1 的其他结点。

从图中某个顶点 v0 出发，首先访问 v0;
依次访问 v0 的各个未被访问的邻接点。
依次从上述邻接点出发，访问他们的各个未被访问的邻接点。始终保证一点：如果 vi 在 vk 之前被访问，则 vi 的邻接点应在 vk 的邻接点之前被访问。重复上述步骤，直到所有顶点都被访问到。
如果还有顶点未被访问到，则随机选择一个作为起始点，重复上述过程，直到图中所有顶点都被访问到。

每个顶点至多进一次队列。遍历图的过程实质上是通过边或弧找邻接点的过程，因此 广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同，两者不同之处仅仅在于对顶点访问的顺序不同。

BFS | 标签 - 小马的笔记

单词接龙2 这道题目需要自己先根据 input 构造图的邻接表存储结构，然后再 BFS 遍历，并且要记录记录父节点序列，还要用 visited 标记已访问结点，是练习 BFS 的一个非常好的题目。
LeetCode.126.Word Ladder II 单词接龙 II

LeetCode.102.Binary Tree Level Order Traversal 二叉树的层次遍历
 LeetCode.107.Binary Tree Level Order Traversal II 二叉树自底向上层次遍历

LeetCode.剑指offer.013.机器人的运动范围

多源广度优先搜索

一般的，广度优先搜索都是从一个源点出发向外扩散。
多源广度优先搜索同时从多个源点出发向外扩撒。
如下图所示

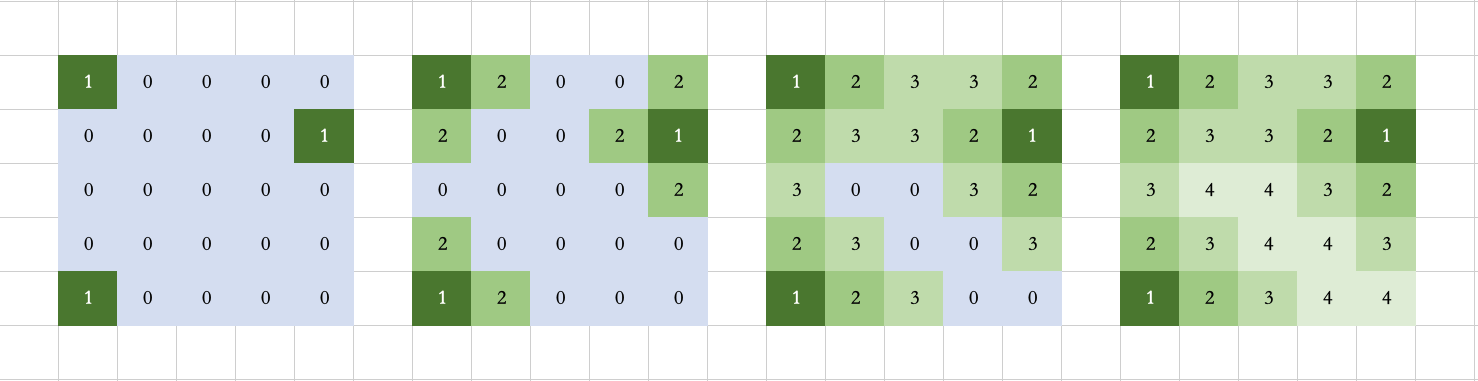
多源广度优先搜索

如何证明理解多源点BFS的正确性？
其实可以通过添加 超级源点 方式来思考。假设所有的源点都以这个超级源点为起点，则其实就相当于我们第一次把这个超级源点添加到队列中，然后从这个超级源点开始搜索一步到达了现在所有的源点。
超级源点可以使多源BFS退化成单源BFS。

推荐使用多源广度优先搜索
因为多源广度优先搜索O(mn) 比进行mn次广度优先搜索O(m^2n^2) 的时间复杂度低两个数量级，某些题虽然两者都能做，但不使用多源广度优先搜索就会超时。
比如
LeetCode.1162.As Far from Land as Possible 离所有陆地最远的海洋/地图分析
这道题不使用多源广度优先搜索是肯定会超时的。

LeetCode.994.Rotting Oranges 腐烂的橘子
 LeetCode.1162.As Far from Land as Possible 离所有陆地最远的海洋/地图分析
 LeetCode.542.01 Matrix 01矩阵

二叉树层次遍历

利用队列做层次遍历，每次先获取当前 queue 的 size，则此时队列的长度一定就是当前层的结点个数，然后一次性取出 size 个结点遍历，完成一层遍历。

LeetCode.102.Binary Tree Level Order Traversal 二叉树的层次遍历
 LeetCode.107.Binary Tree Level Order Traversal II 二叉树自底向上层次遍历
103 Binary Tree Zigzag Level Order Traversal
https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal/

visited[i][j]标记已访问结点

深度/广度优先搜索过程中，我们需要一个数组 visited[m][n] 来记录结点是否访问过

1、直接在原二维数组上标记是否已访问
有的题目是在二维数组中搜索，如果访问过的结点不会再使用，可以原地做标记，直接修改 graph[i][j] 的值来标记是否访问过。
LeetCode.200.Number of Islands 岛屿个数
 LeetCode.695.Max Area of Island 岛屿的最大面积

2、需要额外的 visited[][] 标记是否已访问
在 Java 中的话，可以用 Set<Pair<Integer, Integer>> visited = new HashSet<>(); 集合保存 Pair 来标识已访问过。
LeetCode.542.01 Matrix 01矩阵
 LeetCode.剑指offer.013.机器人的运动范围
 LeetCode.365.Water and Jug Problem 水壶问题
 LeetCode.126.Word Ladder II 单词接龙 II

或者用一个长度为2的数组的集合 Set<Pair<Integer, Integer>> visited = new HashSet<>(); 标记已访问结点
LeetCode.221.Maximal Square 最大正方形

遍历过程中记录父节点序列

保存每个结点的父节点序列，也就是 Queue 中存储的是 List，每个 List 的最后一个节点是当前要遍历的结点。
LeetCode.126.Word Ladder II 单词接龙 II

DFS和BFS比较

一般来说用DFS解决的问题都可以用BFS来解决。

DFS编写容易，可用递归，DFS容易栈溢出，
DFS常用于连通性问题。

BFS没有栈溢出的风险。
BFS多用于最短路径问题。

DFS BFS 效率对比
比如下面这道题中，DFS 比 BFS 要快，能多通过几个超时的大用例
LeetCode.055.Jump Game 跳跃游戏

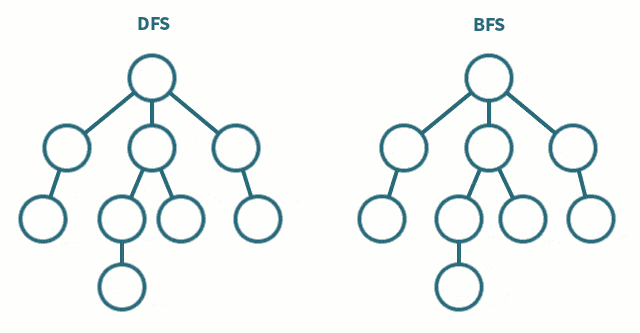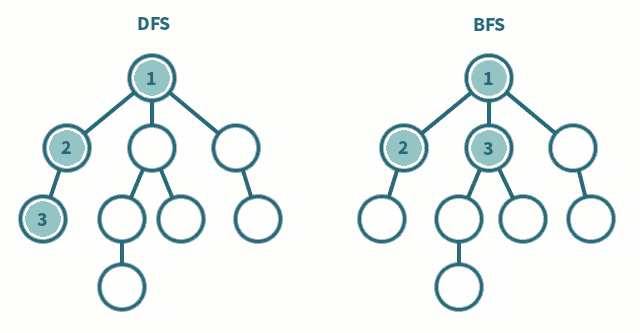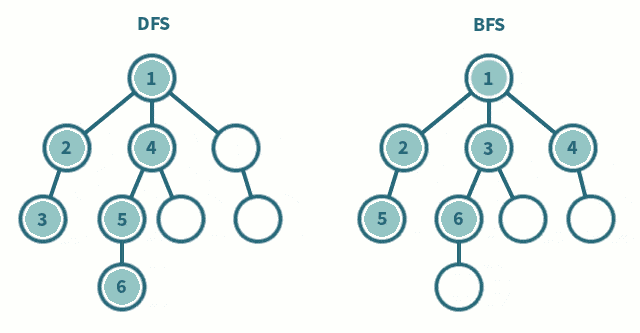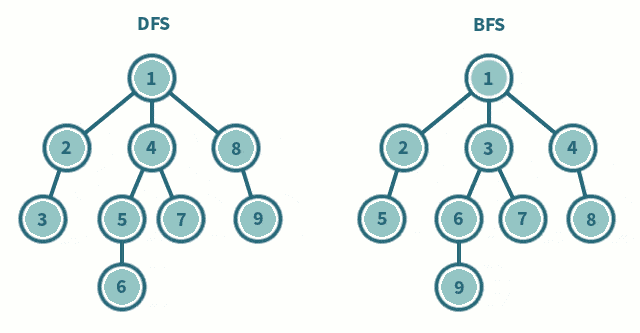
DFS VS BFS

判断图的连通性(DFS/BFS)

如果一个图是连通的，那么从一个节点开始访问，采用深度优先或者广度优先对它进行遍历，那么必定能够访问完所有的节点。

EOJ 1816 判断图连通的三种方法——dfs，bfs，并查集
http://blog.csdn.net/fangpinlei/article/details/42127055

最短路径

无权图最短路径(BFS)

求从顶点A到B所含边数目最少的路径
只需从顶点A出发对图作广度优先搜索，一旦遇到顶点B就终止，此时得到从A到B的最短路径。

一个无权图G，使用某个顶点s作为输入参数，我们想要找出从s到所有其它顶点的最短路径。
这种搜索图的方法称为广度优先搜索（breadth-first search）。该方法按层处理顶点：距开始点最近的那些顶点首先被求值，而最远的那些顶点最后被求值。这很像对树的层序遍历

最短路径算法–无权最短路径
http://blog.csdn.net/tanga842428/article/details/52582817

迪杰斯特拉算法(单源最短路径/贪心)

从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径

迪杰斯特拉算法用于求带权有向图G0中从v0到其余各顶点的最短路径。
注意，迪杰斯特拉算法要求权值为正，如果有负数权值，则迪杰斯特拉算法不再适用，需要用SPFA算法。

地杰斯特拉算法也适用于带权无向图，因为带权无向图可以看作是有往返二重边的有向图，只要在顶点vi 与vj 之间存在无向边(vi , vj )，就可以看成是在这两个顶点之间存在权值相同的两条有向边(vi , vj)和(vj , vi)

算法的思路：
Dijkstra算法是一种 贪心算法，是一种广度优先搜索
数组 dis[] 来保存源点到各个顶点的最短距离
集合T 已经找到了最短路径的顶点的集合
初始时，原点 s 的路径权重被赋为 0 （dis[s] = 0），若对于顶点 s 存在能直接到达的边（s,m），则把dis[m]设为w（s, m）, 同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。初始时，集合T只有顶点s。
然后，从dis数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，OK，此时完成一个顶点，
然后，我们需要看看新加入的顶点是否可以到达其他顶点，并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值。
然后，又从dis中找出最小值，重复上述动作，直到T中包含了图的所有顶点。

设T是已求得最短路径的终点的集合，则可证明：下一条最短路径（设其终点为x）或者是边(s,x)(s为起点)，或者是中间只经过T中顶点到达x的路径。
反证法：假设此路径上有一个顶点不在T中，则说明存在一条终点不在T中而长度比此路径短的路径。但是，这是不可能的。因为我们是按路径长度递增的次序来产生各最短路径的，故长度比此路径短的所有路径均已产生，他们的终点必定在T中，所以假设不成立。

时间复杂度 O(n^2)，空间复杂度 O(n)

最短路径问题—Dijkstra算法详解
https://blog.csdn.net/qq_35644234/article/details/60870719

弗洛伊德算法(多源最短路径/贪心)

依次以图中每个顶点为起点，重复n此迪杰斯特拉算法，可得到每一对顶点间的最短路径，复杂度为 O(n^3)
弗洛伊德算法，用于求赋权图的多源最短路径，也就是图中任意两顶点之间的最短路径，复杂度也是 O(n^3) ，但形式上更简单。

基本思想：
对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。
如果要让任意两点（例如从顶点 a 点到顶点 b）之间的路程变短，只能引入第三个点（顶点 k），并通过这个顶点 k 中转即 a->k->b，才可能缩短原来从顶点 a 点到顶点 b 的路程。

把图用邻接矩阵G表示出来，如果从Vi到Vj有路可达，则G[i][j]=d，d表示该路的长度；否则G[i][j]=无穷大。
定义一个矩阵D用来记录所插入点的信息，D[i][j]表示从Vi到Vj需要经过的点，初始化D[i][j]=j。
把各个顶点插入图中，比较插点后的距离与原来的距离，G[i][j] = min( G[i][j], G[i][k]+G[k][j] )，如果G[i][j]的值变小，则D[i][j]=k。在G中包含有两点之间最短道路的信息，而在D中则包含了最短通路径的信息。
比如，要寻找从V5到V1的路径。根据D，假如D(5,1)=3则说明从V5到V1经过V3，路径为{V5,V3,V1}，如果D(5,3)=3，说明V5与V3直接相连，如果D(3,1)=1，说明V3与V1直接相连。

算法 6：只有五行的 Floyd 最短路算法
https://wiki.jikexueyuan.com/project/easy-learn-algorithm/floyd.html

Bellman-Ford算法

Dijkstra算法是处理单源最短路径的有效算法，但它局限于边的权值非负的情况，若图中出现权值为负的边，Dijkstra算法就会失效，求出的最短路径就可能是错的。
这时候，就需要使用其他的算法来求解最短路径，Bellman-Ford算法就是其中最常用的一个。该算法由美国数学家理查德•贝尔曼（Richard Bellman, 动态规划的提出者）和小莱斯特•福特（Lester Ford）发明。

SPFA算法是Bellman-Ford的队列优化。

SPFA 算法

Shortest Path Faster Algorithm SPFA 算法，通常用于求含负权边的单源最短路径。SPFA算法是Bellman-Ford的队列优化。
迪杰斯特拉算法要求权值为正，如果有负数权值，则迪杰斯特拉算法不再适用，需要用SPFA算法。

最小生成树MST

连通图：在无向图中，若任意两个顶点 vi 与 vj 都有路径相通，则称该无向图为连通图。

强连通图：在有向图中，若任意两个顶点 vi 与 vj 都有路径相通，则称该有向图为强连通图。

连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。

生成树(Spanning Tree): 一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最小生成树(Minimum Spannirng Tree, MST): 在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

Kruskal算法(选边/贪心)

此算法可以称为加边法，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

把图中的所有边按代价从小到大排序；
把图中的n个顶点看成独立的n棵树组成的森林；
按权值从小到大选择边，所选的边连接的两个顶点 ui,vi 应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

时间复杂度 O(eloge)，其中 e 是图中的边个数，与顶点个数无关，所以适合求边稀疏的带权图的最小生成树。

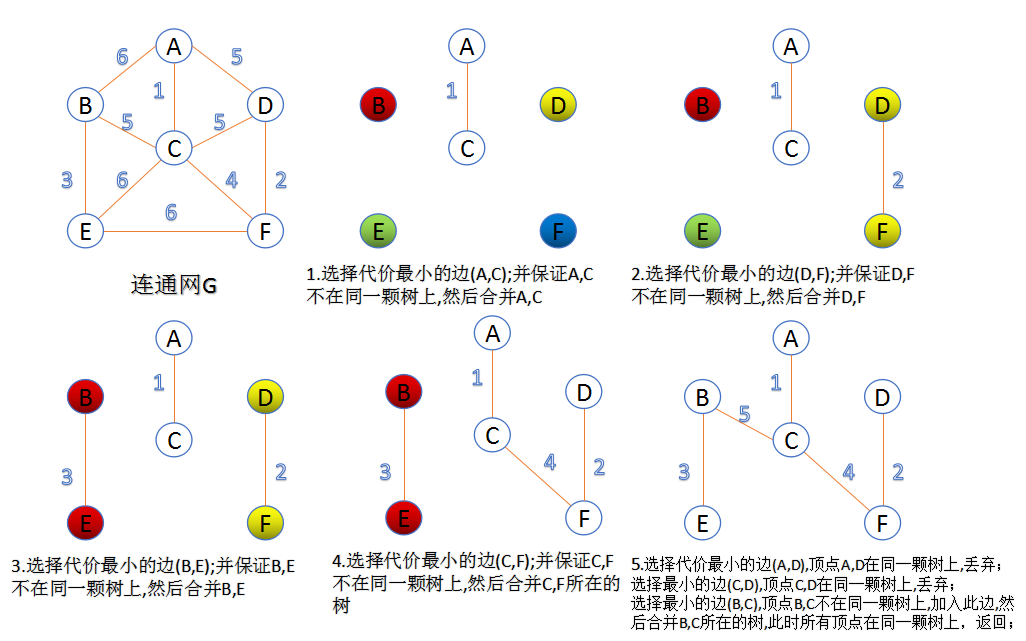
Kruskal算法

Prim算法(选点/贪心)

此算法可以称为加点法，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点 u0 开始，逐渐长大覆盖整个连通网的所有顶点。

图的所有顶点集合为V，所有边的集合为E；初始令顶点集合 $U={u_0}$ ，边集合 $TE={}$
在所有 $u \in U$ 和 $v \in V-U$ 的边 $(u, v) \in E$ 中选择一条代价最小的边 $(u_0, v_0)$ ，把点 $v_0$ 加入集合 U 中，把边 $(u_0, v_0)$ 加入边集 TE 中。
重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止，此时 (V, TE) 就是最小生成树。

Prim算法需要建立一个辅助数组 closedge, 用来维护集合 V-U 中每个顶点与集合 U 中最小代价边信息，closedge 数组中每个元素有两个域 vertex, cost ，vertex 表示到 U 中哪个顶点代价最小， cost 表示这个最小代价，每次新从 V-U 中选择一个点加入 U 后，要同步更新 closedge 数组中所有剩余信息。

时间复杂度 O(n^2)，其中 n 是图中的顶点个数，与图中的边个数无关，所以适合求边稠密的带权图的最小生成树。

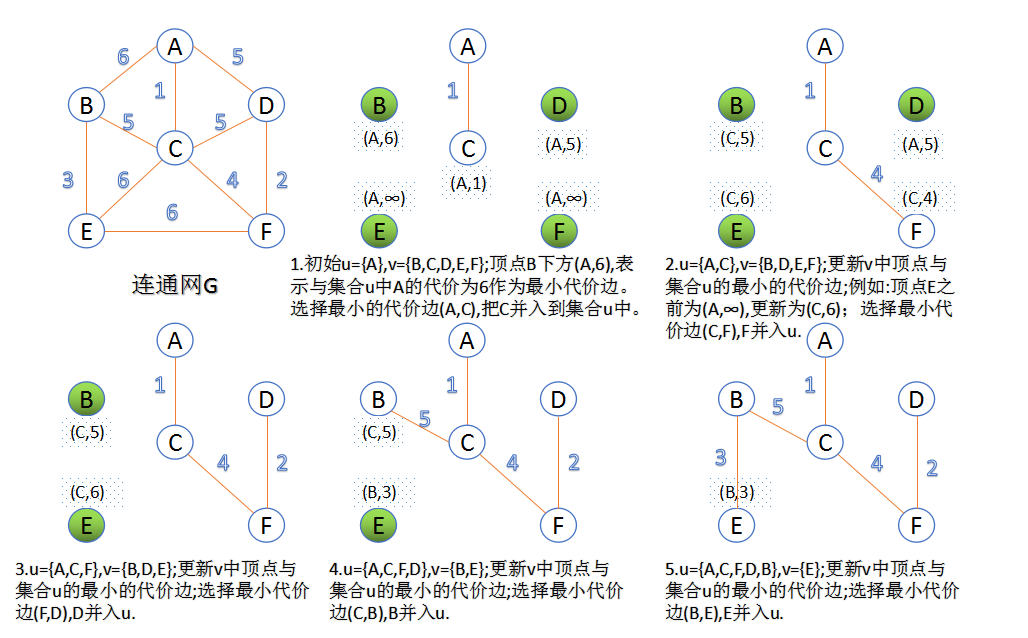
Prim算法

算法导论–最小生成树（Kruskal和Prim算法）
https://blog.csdn.net/luoshixian099/article/details/51908175

有向无环图与拓扑排序

LeetCode.210.Course Schedule II 课程表 II

欧拉回路(七桥问题/一笔画问题)(边)

如下图，一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。

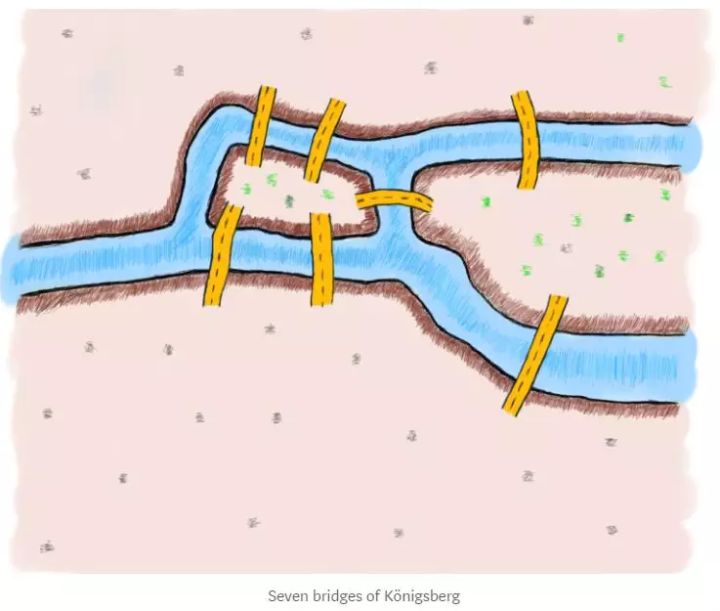
哥尼斯堡七桥问题

注：关于七桥问题，有的描述要求回到起点，有的不要求回到起点，要求回到起点就是找欧拉回路，不要求回到起点就是找欧拉路径。

哥尼斯堡七桥问题
如果要求回到起点，就是判断图中有没有一条欧拉回路，条件是所有结点度数必须为偶数。
如果不要求回到起点，就等同于一笔画问题，就是判断图中有没有欧拉路径，不要求回到起点。只有0个或两个顶点是奇度数，其余都是偶数度的则可以一笔画完。如果全是偶度数结点，以任意结点为起点，一定能以此节点为终点结束。如果有2个奇度数结点，以其中一个奇度数结点为起点，一定能以另一个奇度数结点为重点结束。

图G中经过每条边一次且仅一次的路径叫做欧拉路径。
图G中经过每条边一次且仅一次的回路叫做欧拉回路(Euler Circuit)。
有欧拉回路的图称为欧拉图。

判断欧拉路是否存在的方法
无向图：图连通，只有0个或两个顶点是奇数度，其余都是偶数度的。
有向图：图连通，有一个顶点出度大入度1，有一个顶点入度大出度1，其余都是出度=入度。

判断欧拉回路是否存在的方法
无向图：图连通，所有顶点都是偶数度。
有向图：图连通，所有的顶点出度=入度。

定理：有且仅有两个确定的节点存在奇数自由度，其它的节点都有偶数自由度，那么该有限无向图为 Euler 图。

从七桥问题开始：全面介绍图论及其应用
https://zhuanlan.zhihu.com/p/34442520

哈密尔顿回路(点)

图G中经过每个顶点一次且仅一次的路径叫做哈密尔顿路径
图G中经过每个顶点一次且仅一次的回路叫做 哈密尔顿回路(Hamilton Cycle)
有哈密尔顿回路的图称为哈密尔顿图

哈密尔顿回路与欧拉回路的区别：欧拉回路要求经过所有边，哈密尔顿回路要求经过所有点。

哈密顿路径问题在上世纪七十年代初被证明是“NP完全”的。

二分图

二分图(Bipartite Graph)又称作二部图，是图论中的一种特殊模型。
设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边 (i,j) 所关联的两个顶点i和j分别属于这两个不同的顶点集，则称图G为一个二分图。

简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集。fig1是一个二分图，转化为fig2的形式看着更清楚。

匹配：在图论中，一个匹配（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是匹配。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完全匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

匈牙利算法 用于求解一个二分图的最大匹配问题。

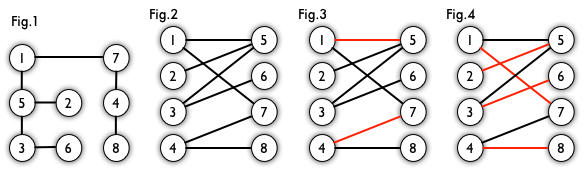
二分图

应用
例1
如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

例2
facebook用户都是双向的好友，a是b的好友，那么b一定是a的好友，现在给定一个用户列表，其中有些用户是好友，有些不是，请判断，这些用户是否可以划分为两组，并且每组内的用户，互相都不是好友。如果能，请给出这个划分。
facebook的好友关系是双向的，意味着是无向图（新浪微博，twitter都是有向图）。然后，要把图划分为两组，这两组满足什么条件呢？组内没有边，组间有边。这显然就是一个二分图。
那问题很明显了，就是facebook好友关系构成的图，是否是一个二分图？如果是，请找到这个划分。就是二分图判断+找到一个划分即可。

二分图的最大匹配、完美匹配和匈牙利算法
https://www.renfei.org/blog/bipartite-matching.html

二分图简介
https://www.cnblogs.com/youxin/p/3352087.html

数学

数学 | 标签 - 小马的笔记

基本运算

整数的位数

正整数 n 的位数等于 $\lfloor log_{10} n \rfloor + 1$，即 log10(n) 向下取整加 1

加减乘除

快速乘(俄罗斯农民乘法)

LeetCode.剑指offer.064.计算1到n的和

快速乘，又叫俄罗斯农民乘法，或俄国农夫法、俄式乘法，它是对两个正整数相乘的一种算法。
注意：快速乘只适用于正整数乘法，如果有负数可以先计算两数绝对值的乘法，再补符号。

一、原理
假设 m 和 n 是两个正整数，计算 m * n
当 n 为偶数时，m * n = 2m * n/2，当 n 为奇数时，m * n = 2m * (n-1)/2 + m

二、手算过程
1、把 m 和 n 两个数字分别写在列头
2、将第一列的数字加倍，将第二列的数字减半。如果在第二列的数字是奇数，将它除以二并把余数去掉。如果第二列的数字是偶数，将其所在行删除。
3、继续加倍、减半和删除直到第二列的数字为1。
4、将第一列中剩余的数字相加。于是就得出了根据原始数字计算出的结果。

其实第 2 步的奇偶处理，就是因为：当 n 为偶数时，m * n = 2m * n/2，当 n 为奇数时，m * n = 2m * (n-1)/2 + m

三、手算过程示例
以计算 57 乘以 86 为例
~~ 57 86~~
114 43
228 21
~~ 456 10~~
912 5
~~1824 2~~
3648 1
第一列上除了已删除的数之外所有数的和为 114 + 228 + 912 + 3648 = 4902，就是最终的结果

或者直接用乘法分配律做变换，也能看出计算过程：

35×37
=34×37+37
=17×74+37
=16×74+74+37
=8×148+111
=4×296+111
=2×592+111
=1×1184+111
=1295

快速乘法代码实现

计算 m × n

令结果 res = 0
当 n 为偶数时，res 值不变，当 n 为奇数时，res == m
m 乘以 2，n 除以 2
n >= 1 时，重复步骤 2-3

// 俄罗斯农民乘法
public long russianFarmerMultiple(long a, long b) {
    // a 不断乘 2， b 不断除以 2，b 是奇数时结果加上 a
    long res = 0;
    while (b >= 1) {
        if (b % 2 == 1) {
            res += a;
        }
        a <<= 1; // a 左移 1 位，即 a 乘 2
        b >>= 1; // b 右移 1 位，即 b 除以 2
    }
    return res;
}

快速乘计算 m*n % k 避免中间结果溢出

利用快速乘法计算 m*n % k 需要先知道两个求余的运算规则，否则看代码会比较费解
1、根据求余运算的加法分配律 (a + b) % p = (a % p + b % p) % p 可知，对加法的中间结果求余和对最终结果求余是一样的，每次对中间结果求余会让中间结果始终小于 k，避免溢出。
2、根据求余运算的乘法结合律 (a * b) % p = ((a % p) * b) % p 可知，被乘数或乘数先求一次余数和对最终结果再求余数结果是相同的，我们每次可以对乘 2 后的被乘数 a 都求一次余数再赋值给 a，让 a 永远小于 k，从而避免溢出。

// 快速乘法计算 m*n mod k 避免中间结果溢出
public long multipleMod(long a, long b, long k) {
    long res = 0;
    while (b >= 1) {
        if (b % 2 == 1) {
            res = (res + a) % k; // 根据求余运算的加法分配律，可对中间结果先求余
        }
        a = (a << 1) % k; // 根据求余运算的乘法结合律，可以对被乘数先求余
        b >>= 1;
    }
    return res;
}

优点：
1、俄罗斯农民乘法表面上看，步骤很多，很笨拙，但其实是极其迅速的。尤其到了计算机二进制的时代，因为在计算机中，除以 2 或者乘以 2 很多时候是不需要计算的，只需左右移位即可。
假设两个 n 位数相乘，普通乘法的时间复杂度为 O(n^2)，俄罗斯农民乘法的时间复杂度为 O(nlogn)

2、对于 (m * n) % k 这种乘法结果取模运算，很可能出现最终结果不溢出但 m * n 这个中间结果溢出的情况，使用俄罗斯农民乘法可以在加法运算过程中不断取模，避免中间结果溢出。

快速幂

LeetCode.050.Pow(x,n) 实现Pow(x,n)

二分搜索开根号

LeetCode.069.Sqrt(x) x的平方根

求余和取模

求余运算规则

n % p 结果的正负由被除数 n 决定，与 p 无关。

加法分配律 (a + b) % p = (a % p + b % p) % p
减法分配律 (a - b) % p = (a % p - b % p) % p
乘法分配律和结合律 (a * b) % p = (a % p) * (b % p) % p = ((a % p) * b) % p
(a ^ b) % p = ((a % p) ^ b) % p

推导 (a * b) % p = ((a % p) * b) % p
把 a 写作 a = (i × p + j) ，即 i 倍的 p 加余数 j
则有 a × b = (ip + j) × b = ibp + jb
所以 (a × b) % p = (ibp + jb) % p = jb % p = ((a % p) × b) % p，其中的 j 就是 a 除以 p 的余数，即 j = a % p

同余定理

数学上，两个整数除以同一个整数，若得相同余数，则二整数同余。
两个整数 a,b，若它们除以整数 m 所得的余数相等，则称 a 与 b 对于模 m 同余，记做 a ≡ b (mod m)

同余定理：如果 a-b 能够被 m 整除，则 a 和 b 关于 m 同余
用符号表示就是，若 m|(a - b) 则 a ≡ b (mod m)，这就是同余定理，例如 11 ≡ 4 (mod 7), 18 ≡ 4(mod 7)

运算性质

若 a ≡ b(mod p)，对于任意整数 c，有 (a + c) ≡ (b + c)(mod p)
若 a ≡ b(mod p)，对于任意整数 c，有 (a * c) ≡ (b * c)(mod p)
若 a ≡ b(mod p) 且 c ≡ d(mod p)，则有 (a + c) ≡ (b + d)(mod p) 以及 (a - c) ≡ (b - d)(mod p)

LeetCode.974.Subarray Sums Divisible by K 和可被K整除的子数组

中国剩余定理

中国剩余定理(Chinese Remainder Theorem, CRT)

物不知数问题
有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？
即求满足以下条件的整数：除以 3 余 2 ，除以 5 余 3 ，除以 7 余 2。

中国剩余定理
https://oi-wiki.org/math/crt/

求余和取模运算的区别

取模运算(Modulo Operation) 和取余运算(Remainder Operation)，这两个概念有重叠的部分但又不完全一致。取模主要用于计算机术语中，求余则更多是数学概念。
被除数和模数符号相同时(包括同为负的情况)，求余和取模运算结果完全相同。
被除数和模数符号不同时，求余和取模运算计算方式不同，结果不同。

对于整型数 a,b 来说，取模运算 a mod b 和求余运算 a % b 的方法都是：
1、求整数商: c = a/b
2、计算模或者余数: r = a - c*b

当 a 和 b 符号不同时，求模运算和求余运算在第一步获得整数 c 值时的舍入方式不同：
求余运算在计算商值时向 0 方向舍弃小数位(ceil)，结果和被除数 a 符号相同
取模运算在计算商值时向负无穷方向舍弃小数位(floor)，结果和模数 b 符号相同

例如计算 -6 mod 5 和 (-6) % 5
-6 / 5 = -1.2
求余运算中，c 向 0 方向舍入，所以 c = -1，进而 (-6) % 5 = -6 - (-1*5) = -1
取模运算中，c 向负无穷方向舍入，所以 c = -2，进而 -6 mod 5 = -6 - (-2*5) = 4

例如计算 6 mod (-5) 和 6 % (-5)
6/-5 = -1.2
求余运算中，c 向 0 方向舍入，所以 c = -1，进而 6%(-5) = 6 - (-1 * -5) = 1
取模运算中，c 向负无穷方向舍入，所以 c = -2，进而 6 mod (-5) = 6 - (-2 * -5) = -4

c/c++/c#/java/php 中 % 是取余运算
python 中 % 是取模运算

Java中的求余运算`%`和取模运算`Math.floorMod()`

Java 中的 % 运算符是求余运算，Math.floorMod(a,b) 是取模运算。
当被除数和模数符号相同时，求余运算和取模运算相同， a % b == Math.floorMod(a,b)
当被除数和模数符号不同时，求余运算和取模运算不同，求余运算 a % b 结果和被除数 a 符号相同，取模运算 Math.floorMod(a,b) 结果和模数 b 符号相同。

Java 求余运算

// 求余运算
@Test
public void testRemainder() {
    System.out.println((-2) % 5);
    System.out.println((-6) % 5);
    System.out.println((2) % (-5));
    System.out.println((6) % (-5));
    System.out.println((-2) % (-5));
    System.out.println((-6) % (-5));
}

结果

-2
-1
2
1
-2
-1

Java 取模运算

// 取模运算
@Test
public void testMod() {
    System.out.println(Math.floorMod(-2, 5));
    System.out.println(Math.floorMod(-6, 5));
    System.out.println(Math.floorMod(2, -5));
    System.out.println(Math.floorMod(6, -5));
    System.out.println(Math.floorMod(-2, -5));
    System.out.println(Math.floorMod(-6, -5));
}

结果：

3
4
-3
-4
-2
-1

python 中的取模运算

python 中运算符 % 本身就是取模运算。

if __name__ == '__main__':
    print((-2) % 5)
    print((-6) % 5)
    print(2 % (-5))
    print(6 % (-5))
    print((-2) % (-5))
    print((-6) % (-5))

结果

3
4
-3
-4
-2
-1

最大公约数(GCD)

最大公约数(Greatest Common Divisor, GCD)，也称最大公因数(Highest Common Factor, HCF)、最大公因子，指两个或多个整数共有约数中最大的一个。

辗转相除法(欧几里得算法)

欧几里德算法又称辗转相除法，用于计算两个正整数a，b的最大公约数(greatest common divisor, GCD)。

其计算原理依赖于
定理：两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。
即 gcd(a, b) = gcd(b, a mod b)

求解过程：
设 a > b，a 除以 b 得余数 r，不断用余数 r 去除除数 b 直到余数为零，此时除数即为最大公约数。

例如：
a = 15, b = 9
15 % 9 = 6
9 % 6 = 3
6 % 3 = 0
所以 gcd 是 3

假如 b > a 大，例如 a = 9, b = 15，同样适用，只不过第一次求余计算就会把 a b 互换：
9 % 15 = 9
15 % 9 = 6
…

代码
java 递归实现：

int gcd(int m, int n) {
    if(n == 0) {
        return m;
    }
    return gcd(n, m % n)
}

java 迭代实现：

int gcd(int x, int y) {
    while (y != 0) {
        int remain = x % y;
        x = y;
        y = remain;
    }
    return x;
}

假设 a, b 中较大的数为 n，基本运算时间复杂度为 O(1)，那么该程序的时间复杂度为 O(logn)
说明：
有 a > b，则有 a mod b < a/2, 也就是每次求余后的结果至少减少一半，所以这相当于二分搜索，每次砍去一半，所以时间复杂度是 O(logn)

最大公约数 GCD 相关题目：
LeetCode.1071.Greatest Common Divisor of Strings 字符串的最大公因子

LeetCode.914.X of a Kind in a Deck of Cards 卡牌分组

更相减损术

更相减损术，出自于中国古代的《九章算术》，也是一种求最大公约数的算法。
他的原理更加简单：两个正整数a和b（a>b），它们的最大公约数等于 a-b 的差值 c 和较小数 b 的最大公约数。
当 a，b两数相差悬殊时，递归深度会很高，比如 10000 和 1，需要递归 9999 次，效率很低。

当a和b均为偶数，gcb(a,b) = 2 * gcb(a/2, b/2) = 2 * gcb(a>>1, b>>1)
当a为偶数，b为奇数，gcb(a,b) = gcb(a/2, b) = gcb(a>>1, b)
当a为奇数，b为偶数，gcb(a,b) = gcb(a, b/2) = gcb(a, b>>1)
当a和b均为奇数，利用更相减损术运算一次，gcb(a,b) = gcb(b, a-b)，此时a-b必然是偶数，又可以继续进行移位运算。

更相减损术和辗转相除法的主要区别在于前者所使用的运算是“减”，后者是“除”。从算法思想上看，两者并没有本质上的区别，但是在计算过程中，如果遇到一个数很大，另一个数比较小的情况，可能要进行很多次减法才能达到一次除法的效果，从而使得算法的时间复杂度退化为 O(N)，其中N是原先的两个数中较大的一个。相比之下，辗转相除法的时间复杂度稳定于 O(logN)。

最小公倍数

最小公倍数(Least Common Multiple, LCM)
最大公约数 * 最小公倍数＝ a * b

裴蜀定理(贝祖定理)

若a,b是整数, 且a,b的最大公约数是d，即 gcd(a,b)=d，那么对于任意的整数x,y, ax+by都一定是d的倍数。
特别地，一定存在整数x,y，使ax+by=d成立。

LeetCode.365.Water and Jug Problem 水壶问题

指数对数

换底公式用于将多异底对数式转化为同底对数式。

$$ \log_a b = \frac{\log_c b}{\log_c a} = \frac{\ln b}{\ln a} $$

$$ \log_a b = \frac{1}{\log_b a} $$

$$ \log_{a^n} b = \frac{\log_a b}{n} $$

$$ \log_a b^n = n \log_a b $$

$$ \log_{a^n} b^m = \frac{m}{n} \log_a b $$

$$ x = e^{\ln x} $$

$$ a^x = e^{\ln {a^x}} = e^{x \ln a} $$

应用
一般计算器只能求 10 为底的对数和 e 为底的自然对数，所以想求任意底的对数时，可以利用换底公式转换为 10 底对数或自然对数
比如 $ \log_6 7 = \frac{\ln 7}{\ln 6} $

LeetCode.069.Sqrt(x) x的平方根
 LeetCode.050.Pow(x,n) 实现Pow(x,n)

一元二次方程求根公式

一元二次方程 $ ax^2 + bx + c = 0 (a \neq 0) $ 的根与根的判别式有如下关系 $ \Delta = b^2 - 4ac $
当 $ \Delta > 0 $ 时，方程有两个不相等的实数根；
当 $ \Delta = 0 $ 时，方程有两个相等的实数根；
当 $ \Delta < 0 $ 时，方程无实数根，但有2个共轭复根。

求根公式：
$ x_{1,2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} $

两根 $x_1$ $x_2$ 有如下关系
$ x_1 + x_2 = - \frac{b}{a} $
$ x_1x_2 = \frac{c}{a} $

向量

特征向量的距离(相似度)

机器学习中每个特征是一个向量，通过计算两个向量之间的距离可以衡量两个特征的相似度。

曼哈顿距离(L1距离)

曼哈顿距离，又叫 L1 距离或城市区块距离，也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投射的距离总和。
假如在曼哈顿要从一个十字路口开车到另一个十字路口，只能沿固定的直角街道走，此时实际驾驶距离就是曼哈顿距离，这也是曼哈顿距离名称的来源。

二维平面中，(x1, y1) 和 (x2, y2) 之间的曼哈顿距离为
c = |x1 - x2| + |y1 - y2|

欧氏距离(L2距离)

n 维空间中两个向量 $A(a_1,a_2,…,a_n)$ 和 $B(b_1,b_2,…,b_n)$ 之间的欧式距离是：
$$
d(A,B) = \sqrt{\sum_{i=1}^n{(a_i-b_i)^2}}
$$

平面中两点 $(x_1,y_1)$ 和 $(x_2,y_2)$ 之间的直线距离就是欧式距离：
$$
\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}
$$

欧式距离越小相似度越大。

余弦距离

把两个向量看成空间中的两条线段，都是从原点（[0, 0, …]）出发，指向不同的方向。
余弦相似度是利用两个向量之间的夹角的余弦值来衡量两个向量之间的余弦相似度。

n维空间中两个向量 $A(a_1,a_2,…,a_n)$ 和 $B(b_1,b_2,…,b_n)$ 之间的余弦距离是：
$$
\cos \theta = \frac
{\sum_1^n{(a_i \times b_i)}}
{\sqrt{\sum_1^n(a_i^2)} \times \sqrt{\sum_1^n{b_i^2}}}
$$

二维空间中向量 $A(x_1,y_1)$ 和 $B(x_2,y_2)$ 之间的夹角的余弦为
$$
\cos \theta = \frac
{x_1x_2 + y_1y_2}
{\sqrt{x_1^2 + y_1^2} \sqrt{x_2^2 + y_2^2}}
$$

夹角余弦取值范围为 [-1,1], 余弦值越大表示两个向量的夹角越小，相似度也就越大。
当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。

欧氏距离和余弦距离的区别

如果保持A向量不变，B向量朝原方向远离坐标原点移动，那么这个时候余弦距离是保持不变的（因为夹角没有发生变化），而A、B两点的欧式距离在发生改变。

统计两部剧的用户观看行为，用户A的观看向量为(0,1)，用户B为(1,0)；此时二者的余弦距离很大，而欧氏距离很小；我们分析两个用户对于不同视频的偏好，更关注相对差异，显然应当使用余弦距离。

而当分析用户活跃度，以登陆次数(单位:次)和平均观看时长(单位:分钟)作为特征时，余弦距离会认为(1,10)、(10,100)两个用户距离很近；但显然这两个用户活跃度是有着极大差异的，此时我们更关注数值绝对差异，应当使用欧氏距离。

几何

几何 | 标签

84 Largest Rectangle in Histogram
https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

线段的交集(区间的交集)

区间 [left1, right1] [left2, right2] 的重叠长度，也就是 两个区间左边界的最大值和右边界的最小值之间的距离，如果左边界最大值大于右边界最小值，则不重叠。

// 计算区间 [left1, right1] [left2, right2] 之间的重叠长度，不重叠返回0
private int overlap(int left1, int right1, int left2, int right2) {
    return Math.min(right1, right2) >= Math.max(left1, left2) ? Math.min(right1, right2) - Math.max(left1, left2) : 0;
}

判断线段 segment1 和 segment2 是否相交

// 判断线段 segment1 和 segment2 是否相交
private boolean isIntersect(int[] segment1, int[] segment2) {
    return Math.max(segment1[0], segment2[0]) <= Math.min(segment1[1], segment2[1]);
}

LeetCode.836.Rectangle Overlap 矩形重叠
 LeetCode.056.Merge Intervals 合并重叠区间
 LeetCode.452.Minimum Number of Arrows to Burst Balloons 用最少数量的箭引爆气球

数列

等差数列

等差数列 ${a_n}$ 的通项公式为 $a_n=a_1+(n-1)d$
前n项和公式为

$$
S_n = a_1 + a_2 + … + a_n = \frac{n(a_1 + a_n)}{2}
$$

或

$$
S_n = a_1 + a_2 + … + a_n = na_1 + \frac{n(n-1)}{2}d
$$

LeetCode.1103.Distribute Candies to People 等差数列分糖果
 LeetCode.剑指offer.057.和为s的连续正数序列

等比数列

矩阵/行列式

转置矩阵

将矩阵的行列互换得到的新矩阵称为转置矩阵，转置矩阵的行列式不变。
把 $m \times n$ 矩阵的 $A$ 行列互换后得到其转置矩阵，记作 $ A^T $
由定义可知，$A$ 为 $m \times n$ 矩阵，则 $ A^T $ 为 $n \times m$ 矩阵

$
A =
\begin{bmatrix}
1 & 0 & 2 \\
-2 & 1 & 3 \\
\end{bmatrix}
$
则
$
A^T =
\begin{bmatrix}
1 & -2 \\
0 & 1 \\
2 & 3 \\
\end{bmatrix}
$

矩阵转置的运算性质
$ (AB)^T = B^T A^T $

旋转矩阵

LeetCode.程序员面试金典.0107.Rotate Matrix 旋转矩阵

54 螺旋矩阵
https://leetcode-cn.com/problems/spiral-matrix/

排列组合

排列

排列: 从n个不同元素中，任取m(m≤n,m与n均为自然数）个不同的元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列，所有可能的排列个数记为 $ A(n, m) $，或 $ A_n^m $ ， A 代表 Arrangement

$ A(n, m) = A_n^m = n(n-1)…(n-m+1) = \frac{n!}{(n-m)!} $

全排列：从n个元素中取出m个元素进行排列，当n=m时这个排列被称为全排列，n个元素的全排列共有 n! 个

46 全排列
https://leetcode-cn.com/problems/permutations/

组合

组合: 从n个不同元素中，任取m(m≤n,m与n均为自然数）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合，所有可能的组合个数记为 $C(n, m)$ 或 $ C_n^m $， C 代表 Combination

$ C(n, m) = C_n^m = \frac{A_n^m}{m!} = \frac{n!}{(n-m)!m!} $

幂集

幂集: 一个集合 S 的所有子集组成的集合，叫做 S 的幂集，记为 P(S)
如果集合 S 的元素个数为 n ，则其幂集的元素个数为 2^n

$ C_n^0 + C_n^1 + … + C_n^n = 2^n $

二项式定理

$ (a + b)^n = \sum_{i = 0}^n C_n^i a^{n-i} b^i $

当前位置 : 首页 » 文章分类 : 算法 » 面试准备15-算法

算法相关博客和书籍

labuladong的算法小抄

LeetCode 问题分类讲解 - liweiwei

负雪明烛的刷题博客

程序员小灰的博客

OI Wiki

剑指offer题解 - 心谭博客

LeetCode题解 - lucifer

LeetCode题解 - windliang

小马的笔记

书籍

算法与技巧

逻辑运算的短路特性

位运算

利用a^a=0消除元素

利用某bit位上的差异区分不同元素

异或是无进位的加号

-i等于i各位取反加1:-i==~i+1

分离最右边的1:i&(-i)

将最右边的1设为0:x&(x-1)

位运算技巧总结

循环左移/右移n位

不引入新变量交换两个数的值

加法

异或

利用int的空闲bit位保存需要的信息

双指针

滑动窗口/快慢指针

左右指针/前后指针

前后指针+交换

前后双指针根据条件向中间逼近

排序+双指针

两个数组(链表)中的双指针

倍速指针

k间隔指针

交替互换指针

二分搜索

旋转有序数组中的二分搜索

山脉数组(先升后降)中的二分搜索

两个数组中的二分搜索

二分搜索计算mid的经典bug

Java中的Arrays.binarySearch()的bug与修复

分治法

归并排序

数组中的逆序对

合并K个排序链表

315 计算右侧小于当前元素的个数

线段树

回溯法

回溯法的代码模板DFS

回溯法中什么情况下需要回退(撤销选择)？

排列组合

全排列(经典回溯模板)

括号生成

78 子集(经典回溯模板)

贪心算法

跳跃游戏

区间重叠问题

用最少数量的箭引爆气球

合并重叠区间

最大重叠区间数目

最大重叠区间大小

集合覆盖问题

动态规划

斐波那契数列

爬楼梯

约瑟夫环

最长公共子序列LCS

最长公共子串LCS/最长重复子数组

最长有效括号子串

最长上升子序列LIS

最大连续子序列和

最大连续子序列积

最大非相邻子序列和(打家劫舍/按摩师)

最长回文子串

零钱兑换-最少硬币数

零钱兑换-总方案数

编辑距离

鸡蛋掉落问题

利用`a^a=0`消除元素

-i等于i各位取反加1:`-i==~i+1`

分离最右边的1:`i&(-i)`

将最右边的1设为0:`x&(x-1)`

`1 ≤ a[i] ≤ n`值在下标范围内

`'a' ≤ a[i] ≤ 'z'`值只包含大小写字母